Вопрос 22. Решение матричных игр с нулевой суммой для игр с седловой точкой

Парная игра (т.е. в которой участвуют два разумных игрока) называется игрой с нулевой суммой, если выигрыш одного игрока равен проигрышу другого.

Рассмотрим игру 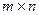, в которой игрок А имеет личных стратегий, а игрок В («противник») – личных стратегий. Стратегии игрока А будем обозначать , противника – . Предположим, что каждая сторона выбрала определенную стратегию: мы выбрали , противник . В результате выбора игроками любой пары стратегий A_i, B_j (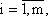 ) однозначно определяется исход игры, т.е. выигрыш a_ij игрока А (положительный или отрицательный) и проигрыш (- a_ij) игрока В.

Предположим, что нам известны значения для каждой пары стратегий. Эти значения можно записать в виде прямоугольной таблицы или матрицы.

Матричная игра – это парная игра с нулевой суммой, описанная в виде платежной матрицы.

Матрица А = (a_ij), 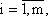, элементами которой являются выигрыши, соответствующие стратегиям A_i и B_j, называется платежной матрицей или матрицей игры.

Общий вид платежной матрицы приведен ниже:

… … …   … … … … … … …

В платежной матрице приведены числа 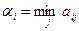– минимально возможный выигрыш игрока А, применяющего стратегию () и – максимально возможный проигрыш игрока В, если он пользуется стратегией (). Чистая стратегия – это некоторая стратегия игрока, выбранная им с вероятностью, равной 1.

Поскольку инте­ресы игроков противоположны, то первый игрок стремится макси­мизировать свой выигрыш, а второй игрок, наоборот, минимизиро­вать свой проигрыш.

Число называют нижней ценой игры (максимином), а соответствующую ему чистую стратегию – максиминной.

Число показывает, какой минимальный гарантированный выигрыш может получить игрок А, правильно применяя свои чистые стратегии при любых действиях игрока В.

Число называют верхней ценой игры (минимаксом), а соответствующую чистую стратегию минимаксной.

Число 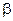показывает, какой минимальный гарантированный проигрыш может быть у игрока В, при правильном выборе им своих чистых стратегий независимо от действий игрока А. (Ясно, что .)

Игры, для которых нижняя цена равна верхней, т.е. 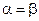, называются играми с седловой точкой. Общее значение верхней и нижней цены v = α = β называется чистой ценой игры, или просто ценой игры. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях и имеет чистую цену игры v = α = β. Максиминная 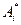и минимаксная стратегии, образующие седловую точку, являются оптимальными стратегиями. Тройку чисел (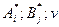) называют решением игры.

Седловая точка есть точ­ка равновесия игры, определяющая однозначно оптимальные стра­тегии. Оптимальность здесь означает, что ни один игрок не стре­мится изменить свою стратегию, так как его противник может на это ответить выбором другой стратегии, дающей худший для пер­вого игрока результат.

Пример. Проверим наличие седловой точки в игре, заданной платежной матрицей.

				min
max

Решение. Для игрока А максимин: = max (1, 1, 10) = 10.

Для игрока В минимакс: = min(10, 10, 12) = 10.

Решение игры – две седловые точки: (А ₃, В ₁, 10), (А ₃, В ₂, 10).

Оптимальный выбор для игрока 1 – стратегия А ₃, для игрока 2 равнозначны стратегии В _{1 И} В ₂.

Не нашли, что искали? Воспользуйтесь поиском: