Решение матричных игр с нулевой суммой для игр без седловой точки

Таким образом, для игры с седловой точкой нахождение решения заключается в выборе максиминной и минимаксной стратегии, которые и являются оптимальными.

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В этом случае можно получить оптимальное решение, используя смешанные стратегии.

Смешанной стратегией называется сложная стратегия, состоящая в случайном применении стратегий из всего набора стратегий игрока с определенными вероятностями.

Смешанной стратегией игрока А называется применение чистых стратегий А ₁, А ₂, …, А_m c вероятностями р ₁, р ₂, …, р_m.

Смешанной стратегией игрока В называется применение чистых стратегий В ₁, В ₂, …, В_n c вероятностями q ₁, q ₂, …, q_n.

Обычно смешанную стратегию первого игрока обозначают как вектор: , а стратегию второго игрока как вектор: .

Оптимальное решение игры – это пара оптимальных стратегий , , в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству: α ≤ v ≤ β.

Оптимальные смешанные стратегии и игроков А и В могут быть найдены в результате решения пары двойственных задач линейного программирования.

Для игрока А: Для игрока В:

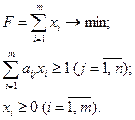
В результате решения задачи для игрока А находятся оптимальный вектор и экстремум целевой функции , а затем цена игры и компоненты вектора вероятностей применения игроком А своих стратегий .

Решая задачу для игрока В, находят оптимальный вектор и экстремум целевой функции , а затем цену игры и компоненты вектора вероятностей применения игроком В своих стратегий .

Цель игрока А – максимизировать свой гарантированный выигрыш, т.е. цену игры v. Максимизация цены игры v эквивалентна минимизации значения целевой функции F (), поэтому целевая функция задачи для игрока А должнаобращаться в минимум.

Цель игрока В – минимизировать свой гарантированный проигрыш, т.е. цену игры v. Минимизация цены игры v эквивалентна максимизации значения целевой функции F (), поэтому целевая функция задачи для игрока В должнаобращаться в максимум.

Пример. Найти решение и цену игры, платежная матрица которой представлена нижеследующей таблицей.

				min
max

Решение. Проверим наличие седловой точки.

Для игрока А максимин: = max (1, 3) = 3.

Для игрока В минимакс: = min(15, 4, 9) = 4.

Так как значения α и β не совпадают, седловой точки нет, а цена игры v находится в промежутке [3; 4].

Решим задачу в смешанных стратегиях. Для этого составим пару двойственных задач.

Для игрока А: Для игрока В:

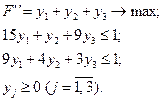
Решим в Excel обе задачи.

Находим экстремум целевой функции для обеих задач – он будет одинаков и равен

для игрока А: F = 0,27. х ₁ = 0,03, х ₂ = 0,24. Теневые цены: 0; 0,18; 0,09;

для игрока В: F = 0,27. у ₁ = 0, у ₂ = 0,18, у ₂ = 0,09. Теневые цены: 0,03; 0,24.

Отсюда находим цену игры

. Полученная цена игры 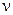находится в промежутке [3; 4].

Находим компоненты вектора вероятностей применения игроком А своих стратегий:

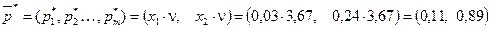. Проверим: .

Находим компоненты вектора вероятностей применения игроком В своих стратегий:

.

Проверим: .

Понимать это решение следует так: если разыгрывается 100 партий игры, то в соответ­ствии с вероятностями применения стратегий игрок А, случайным образом чередуя применение стратегий, должен применить 1-ю стратегию 11 раз, 2-ю – 89 раз. Второй игрок также должен случайным образом чередовать применение своих стратегий и применить 1-ю стратегию 0 раз, 2-ю – 67 раз, 3-ю – 33 раза. В этом случае игрок А за 100 партий игры выиграет 367 единиц, а игрок В эту вели­чину проиграет.

Не нашли, что искали? Воспользуйтесь поиском: