
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Многоканальная СМО с отказами
Для СМО с отказами наиболее важными характеристиками являются:
1) абсолютная пропускная способность A – среднее число заявок, которое может обслужить система за единицу времени.
2) относительная пропускная способность q – вероятность того, что поступившее в систему требование будет принято к обслуживанию (дополняет вероятность отказа 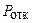 до единицы).
до единицы).
3) в зависимости от задачи исследования могут быть важны и другие характеристики, например, среднее число занятых каналов 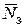 , среднее относительное время простоя системы в целом и отдельного канала и т. д.
, среднее относительное время простоя системы в целом и отдельного канала и т. д.
Если требование поступает в систему в момент, когда все п каналов заняты, то оно получает отказ (покидает систему необслуженным). Если же в момент поступления требования имеется хотя бы один свободный канал, то оно принимается к обслуживанию и обслуживается до конца. Размеченный граф состояний системы с отказами представлен на рисунке.
Пусть СМО содержит п канатов, интенсивность входящего потока заявок равна λ, а интенсивность обслуживания заявки каждым каналом равна μ. Размеченный граф состояний системы изображён на рис. 1.

Рисунок 1 – Граф состояний многоканальной системы с отказами
Состояние S0 означает, что все каналы свободны, состояние Sk (k =  ) означает, что обслуживанием заявок заняты k каналов, остальные свободны, Sn – заняты все п каналов, заявка получает отказ в обслуживании.
) означает, что обслуживанием заявок заняты k каналов, остальные свободны, Sn – заняты все п каналов, заявка получает отказ в обслуживании.
Переход из одного состояния в другое соседнее правое происходит скачкообразно под воздействием входящего потока заявок интенсивностью А независимо от числа работающих каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее левое неважно, какой именно канал освободится. Величина k μхарактеризует интенсивность обслуживания заявок при работе в СМО k каналов (нижние стрелки).
Предельные вероятности состояний системы рассчитываются по формулам Эрланга, которые для рассматриваемой СМО имеют вид:
 (4)
(4)
где Р 0 – вероятность свободного состояния системы, Рk – финальные вероятности состояния системы (вероятности того, что обслуживанием заявок заняты k каналов).
Сумма значений всех найденных по формулам Эрланга вероятностей должна быть равна 1.
Вероятность отказа в обслуживании 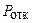 равна вероятности того, что все каналы заняты, т.е. система находится в состоянии
равна вероятности того, что все каналы заняты, т.е. система находится в состоянии  :
: 
Относительная пропускная способность – вероятность того, что заявка будет принята к обслуживанию (дополняет 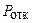 до единицы):
до единицы): 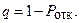
Абсолютная пропускная способность  – среднее число заявок, которое может обслужить СМО в единицу времени: A = λ
– среднее число заявок, которое может обслужить СМО в единицу времени: A = λ  .
.
Среднее число занятых каналов  .
.
Пример 1. На вход многоканальной СМО с отказами поступает поток заявок, интенсивность которого составляет 7 заявок в час. Среднее время обслуживания одной заявки 0,25 часа. Каждая заявка приносит доход 150 ден.ед., а содержание одного канала обходится в 120 ден.ед в час. Найти оптимальное число каналов СМО.
Решение. Основные параметры системы:
1) число каналов n – нужно определить;
2) число мест в очереди m = 1;
3) среднее время обслуживания  =0,25 часа;
=0,25 часа;
4) интенсивность потока заявок l=7 заявок в час;
5) интенсивность обслуживания 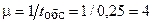 ч–1;
ч–1;
6) относительная нагрузка на систему  заявок.
заявок.
Из условия задачи также вытекает, что в случае, если СМО имеет  каналов, то она приносит доход
каналов, то она приносит доход  , который можно определить по формуле
, который можно определить по формуле  , где
, где  – абсолютная пропускная способность СМО. Дальнейшие расчеты сведены в таблицу 12.1
– абсолютная пропускная способность СМО. Дальнейшие расчеты сведены в таблицу 12.1
Таблица 12.1 – Определение оптимального количества каналов
| Число каналов | Вероятность свободного состояния системы 
| Вероятность отказа 
| Абсолютная пропускная способность  , заявок , заявок
| Доход  ден.ед. ден.ед.
|

| 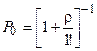 = 0,364 = 0,364
| 0,636 | 2,545 | |

|  =0,234 =0,234
| 0,204 | 5,569 | |

|  =0,193 =0,193
| 0,056 | 6,61 | |

|  =
=0,18 =
=0,18
| 0,013 | 6,91 |
Сравнивая доходы, поступающие от СМО в случаях  , можно отметить, что при увеличении каналов от одного до трех доход растет и становится наибольшим при
, можно отметить, что при увеличении каналов от одного до трех доход растет и становится наибольшим при  . Это значение и является оптимальным количеством каналов.
. Это значение и является оптимальным количеством каналов.
Для многоканальной СМО с неограниченным ожиданием как абсолютная А, так и относительная пропускная способность q теряют смысл, так как каждая поступившая заявка рано или поздно будет обслужена. Зато для такой СМО весьма важными характеристиками являются:
1) среднее число заявок в очереди 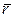 ,
,
2) среднее число заявок в системе  (в очереди и под обслуживанием),
(в очереди и под обслуживанием),
3) среднее время ожидания заявки в очереди 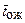 ,
,
4) среднее время пребывания заявки в системе  (в очереди и под обслуживанием), и другие характеристики ожидания.
(в очереди и под обслуживанием), и другие характеристики ожидания.
Так как длина очереди не ограничена, то граф состояний (при  ) в этом случае является бесконечным.
) в этом случае является бесконечным.
 …
…
Рисунок 2 – Граф состояний многоканальной системы с неограниченным ожиданием
Далее представлены формулы для расчета характеристик СМО с неограниченной очередью.
Предельные вероятности состояний:
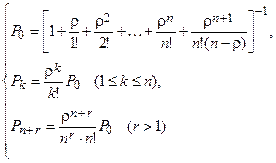 (5)
(5)
где Р 0 – вероятность свободного состояния системы,  – финальные вероятности состояния системы (вероятности того, что обслуживанием заявок заняты k каналов),
– финальные вероятности состояния системы (вероятности того, что обслуживанием заявок заняты k каналов),  – вероятности того, что
– вероятности того, что  заявок находится в очереди при занятом количестве каналов
заявок находится в очереди при занятом количестве каналов  .
.
Сумма значений всех найденных по формулам Эрланга вероятностей должна быть равна 1.
Использование формул (5) является корректным лишь в том случае, когда выполняется условие существования стационарного режима СМО:  . Смысл этого условия состоит в том, что суммарная интенсивность обслуживания, создаваемая всеми n одновременно работающими каналами, равная n μ, должна быть строго больше интенсивности входного потока заявок λ.
. Смысл этого условия состоит в том, что суммарная интенсивность обслуживания, создаваемая всеми n одновременно работающими каналами, равная n μ, должна быть строго больше интенсивности входного потока заявок λ.
Так как число мест в очереди не ограничено, то все требования, поступившие в систему, рано или поздно будут обслужены. Следовательно, вероятность отказа
 .
.
Среднее число занятых каналов
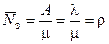 .
.
Среднее число требований, находящихся в очереди

Среднее число требований, находящихся в системе  .
.
Среднее время пребывания требования в очереди  .
.
Среднее время пребывания требования в системе 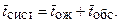
Пример 2. Железнодорожная касса с двумя окошками продает билеты в два пункта А и В. Интенсивность потока пассажиров, желающих купить билеты, для обоих пунктов одинакова: λ А = λ В = 0,45 пассажиров в минуту. На обслуживание пассажиров кассир тратит в среднем 2 мин. Рассматриваются два варианта продажи билетов: первый – билеты продаются в одной кассе с двумя окошками одновременно в оба пункта А и В; второй – билеты продаются в двух специализированных кассах (по одному окошку в каждой), одна только в пункт А, другая – только в пункт В. Необходимо сравнить два варианта продажи билетов по основным характеристикам обслуживания.
Решение.
а) По первому варианту имеем двухканальную СМО с неограниченным ожиданием, на которую поступает поток заявок со следующими параметрами:
1) число каналов n = 2;
2) число мест в очереди  ;
;
3) среднее время обслуживания  = 2 минуты;
= 2 минуты;
4) интенсивность потока заявок l = 0,45 + 0,45 = 0,9 пассажиров в минуту;
5) интенсивность обслуживания 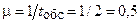 мин–1;
мин–1;
6) относительная нагрузка на систему 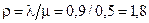 пассажиров.
пассажиров.
Необходимо проверить выполнение условия существования стационарного режима СМО:  . Так как
. Так как  , то использование формул (5) является корректным.
, то использование формул (5) является корректным.
Вероятность простоя двух кассиров
 .
.
Среднее число пассажиров в очереди у кассы
 пассажиров.
пассажиров.
Среднее число пассажиров у кассы  пассажиров.
пассажиров.
Среднее время на ожидание в очереди составляет:  мин.
мин.
Среднее время на покупку билетов составляет:  мин.
мин.
По второму варианту имеем две одноканальные СМО с неограниченным ожиданием (два специализированных окошка), на каждую из которых поступает поток заявок со следующими параметрами:
1) число каналов n = 1;
2) число мест в очереди  ;
;
3) среднее время обслуживания  = 2 минуты;
= 2 минуты;
4) интенсивность потока заявок l = 0,45 пассажиров в минуту;
5) интенсивность обслуживания 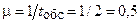 мин–1;
мин–1;
6) относительная нагрузка на систему  пассажиров.
пассажиров.
Необходимо проверить выполнение условия существования стационарного режима СМО:  . Так как
. Так как 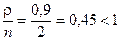 , то использование формул (5) является корректным.
, то использование формул (5) является корректным.
Вероятность простоя одного кассира
 .
.
Среднее число пассажиров в очереди у одного окошка
 пассажира.
пассажира.
Среднее число пассажиров у одного окошка в кассу  пассажиров.
пассажиров.
Среднее время на ожидание в очереди у одного окошка в кассу составляет:  мин.
мин.
Среднее время на покупку билетов составляет:  мин.
мин.
Итак, по второму варианту увеличились и длина очереди, и среднее время ожидания в ней и в целом на покупку билетов. Такое различие объясняется тем, что в первом варианте (двухканальная СМО) меньше средняя доля времени, которую простаивает каждый их двух кассиров, если он не занят обслуживанием пассажира, покупающего билет в пункт А, и он, следовательно, может заняться обслуживанием пассажира, покупающего билет в пункт В, и наоборот. Во втором варианте такой взаимозаменяемости нет.
Можно заметить, что среднее время на покупку билетов по второму варианту увеличилось более чем в 2 раза. Такое значительное увеличение связано с тем, что СМО работает на пределе своих возможностей ( пассажиров): достаточно незначительно увеличить среднее время обслуживания
пассажиров): достаточно незначительно увеличить среднее время обслуживания  , т.е. уменьшить
, т.е. уменьшить 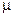 , и относительная нагрузка на систему
, и относительная нагрузка на систему 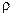 станет больше 1, т.е. очередь начнет неограниченно возрастать.
станет больше 1, т.е. очередь начнет неограниченно возрастать.
Для многоканальной СМО с ограниченным ожиданием интерес представляют обе группы характеристик: как абсолютная и относительная пропускная способности, так и характеристики ожидания.
Пусть в n -канальную СМО поступает простейший поток требований с интенсивностью λ; число мест в очереди ограничено и равно т. Время обслуживания требований (для одного канала) экспоненциальное, со средним значением t обс .
Размеченный граф состояний системы с ограниченной длиной очереди представлен на рисунке.

Рисунок 3 – Граф состояний многоканальной системы с ограниченной длиной очереди
Предельные вероятности состояний системы (формулы Эрланга) имеют вид
 (6)
(6)
где Р 0 – вероятность свободного состояния системы,  – финальные вероятности состояния системы (вероятности того, что обслуживанием заявок заняты k каналов),
– финальные вероятности состояния системы (вероятности того, что обслуживанием заявок заняты k каналов),  – вероятности того, что
– вероятности того, что  заявок находится в очереди при занятом количестве каналов
заявок находится в очереди при занятом количестве каналов  .
.
Сумма значений всех найденных по формулам Эрланга вероятностей должна быть равна 1.
Требование получает отказ в том случае, когда все т мест в очереди заняты, то есть вероятность отказа

Относительная пропускная способность или вероятность того, что поступившее в систему требование будет принято к обслуживанию, дополняет вероятность отказа до единицы:

В систему поступает λ требований в единицу времени, а доля требований, принятых к обслуживанию, равна q. Следовательно, абсолютная пропускная способность

Каждый канал, если он занят, обслуживает в единицу времени mтребований, а вся система – А требований. Таким образом, среднее число занятых каналов
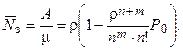
Среднее число требований 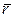 , находящихся в очереди, вычислим как математическое ожидание числа требований, находящихся в очереди:
, находящихся в очереди, вычислим как математическое ожидание числа требований, находящихся в очереди:

Подставив значения Рn+r (r= 1, m) и выполнив преобразования, окончательно получим
 .
.
Учитывая, что среднее число требований, находящихся под обслуживанием, совпадает со средним числом занятых каналов, среднее число требований, находящихся в системе, равно  .
.
Среднее время пребывания требований в очереди
 .
.
Среднее время пребывания заявки в системе

Среднее время пребывания требования в системе получим, если к среднему времени ожидания в очереди прибавим среднее время обслуживания, умноженное на относительную пропускную способность q.
Пример 3. На склад в среднем прибывают 5 машин в час. Разгрузку осуществляют 3 бригады грузчиков. Среднее время разгрузки машины – 1 час. В очереди в ожидании разгрузки могут находиться не более 3-х машин. Найти основные характеристики СМО и оценить эффективность её работы.
Решение. Основные параметры системы: число каналов n = 3 бригады; число мест в очереди m = 3 машины; среднее время обслуживания  =1 час; интенсивность потока заявок l = 5 машин в час; интенсивность обслуживания
=1 час; интенсивность потока заявок l = 5 машин в час; интенсивность обслуживания  час–1; относительная нагрузка на систему
час–1; относительная нагрузка на систему  машин.
машин.
Р 0 – вероятность свободного состояния системы
 т.е. грузчики работают практически без отдыха.
т.е. грузчики работают практически без отдыха.
 – финальные вероятности состояния системы (вероятности того, что обслуживанием заявок заняты k каналов) при
– финальные вероятности состояния системы (вероятности того, что обслуживанием заявок заняты k каналов) при 
 0,022
0,022
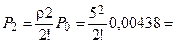 0,055
0,055
 0,091
0,091
 – вероятности того, что
– вероятности того, что  заявок находится в очереди при занятом количестве каналов
заявок находится в очереди при занятом количестве каналов 
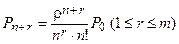
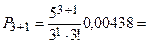 0,152
0,152
 0,253
0,253
 0,422.
0,422.
Проверяем: 0,00438+0,022+0,055+0,091+0,152+0,253+0,422 ≈ 1.
Вероятность отказа в обслуживании прибывшей на склад машины:
 0,422.
0,422.
Т.е. вероятность отказа составляет 42 %.
Относительная пропускная способность равна
 0,578.
0,578.
Т.е. вероятность того, что поступившая на склад машина будет разгружена, составляет 57,8 %.
Абсолютная пропускная способность
 машин в час.
машин в час.
Среднее число машин в очереди находим по формуле
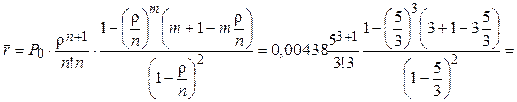 1,926 машин
1,926 машин
машин, т.е. существенно меньше = 4.
Среднее время пребывания машины в очереди находим по формуле
 0,385 ч.
0,385 ч.
Среднее время пребывания машины на складе
 0,963 ч.
0,963 ч.
что сравнимо со средним временем разгрузки машины. Можно сделать вывод, что разгрузка машин на складе организована не слишком эффективно, поскольку вероятность отказа в обслуживании составляет 42 %, и вероятность того, что 3 заявки находится в очереди при занятом количестве каналов  =3, самая большая, т.е. необходимо увеличить количество грузчиков.
=3, самая большая, т.е. необходимо увеличить количество грузчиков.
Не нашли, что искали? Воспользуйтесь поиском: