Системы и модели массового обслуживания

Менеджеру-экономисту часто приходится сталкиваться с ситуациями, которые характеризуются термином системы массового обслуживания. Пример:

1) обслуживание покупателей в сфере розничной торговли

2) транспортное обслуживание

3) медицинское обслуживание населения

4) ремонт аппаратуры, машин, механизмов, находящихся в эксплуатации

5) обработка документов в системе управления

6) туристическое обслуживание (билетные кассы, справочные бюро).

Системы массового обслуживания (СМО) представляют собой структуры, содержащие одно или несколько обслуживающих устройств – каналов обслуживания, на вход которых в случайные моменты времени поступают требования для обслуживания. В качестве каналов могут фигурировать технические устройства либо персонал, выполняющие функции обслуживания.

Требованием или заявкой называется объект, который необходимо обслужить: автомобили, проходящие через шлагбаум, покупатели, приобретающие товар и т.д. Как видно, объект является носителем запроса. Поэтому в дальнейшем под требованием понимается и сам запрос на обслуживание. Например, запрос на ремонт станка, запрос на продажу товара покупателю и т.д.

Совокупность появляющихся требований называется потоком требований.

Каждая СМО предназначена для обслуживания какого-то потока заявок (или «требований»), поступающих на СМО в какие-то случайные моменты времени. Обслуживание поступившей заявки продолжается некоторое (вообще говоря, случайное) время, после чего канал освобождается и готов к принятию следующей заявки. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на входе СМО скапливается излишне большое число заявок (они либо образуют очередь, либо покидают СМО необслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

Система массового обслуживания – это система двух взаимодействующих потоков случайных событий – входного потока заявок (требований) на обслуживание и выходного потока обслуженных требований.

Состояние системы – это число находящихся в СМО заявок в данный момент.

Узел обслуживания – это часть СМО, через который осуществляется взаимодействие входного и выходного потока заявок. Узел обслуживания может содержать один или более обслуживающих каналов (обслуживающих устройств, приборов).

Пример обслуживающего канала – рабочее место кассира на предприятии массового обслуживания. В случае транспортного обслуживания каналом может считаться отдельная единица транспортного средства.

Заявки, находящиеся в СМО, могут либо ожидать обслуживания, либо находиться под обслуживанием.

Очередь – это часть заявок, ожидающих обслуживания.

Дисциплина очереди – это правила формирования очереди.

Каждая система массового обслуживания, в зависимости от числа каналов и их производительности, а также от характера потока заявок, обладает какой-то пропускной способностью, позволяющей ей более или менее успешно справляться с потоком заявок.

Предмет теории массового обслуживания – установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью обслуживания.

Главная особенность процессов массового обслуживания – случайность. Теория массового обслуживания опирается на теорию вероятностей и математическую статистику.

Первоначально развитие теории массового обслуживания связано с именем датского ученого А.К.Эрланга (1878-1929), с его трудами в области проектирования и эксплуатации телефонных станций. Большой вклад в развитие этой теории внесли российские математики А.Я.Хинчин, Б.В.Гнеденко, А.Н.Колмогоров, Е.С. Вентцель и др.

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких систем массового обслуживания, процесс функционирования которых является марковским, то есть все потоки событий, переводящие систему из состояния в состояние, простейшие.

Простейшим называется случайный поток, обладающий тремя основными свойствами: стационарности, ординарности и отсутствия последействия.

Свойство стационарности обеспечивает постоянное количество требований в течение некоторого промежутка. При этом количество требований зависит только от длины этого промежутка по оси времени, т.е. это свойство не учитывает суточные и годовые колебания спроса.

Свойство ординарности указывает, что вероятность поступления двух заявок одновременно является бесконечно малой величиной.

Свойство отсутствия последействия состоит в том, что количество требований, поступивших в систему после времени t ₀ не зависит от числа требований до этого момента.

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, то есть вероятность поступления за время t рóвно k требований задается формулой

, (1)

где λ – плотность потока или среднее число требований в единицу времени.

Заранее условимся (чтобы не оговаривать это всякий раз отдельно), что мы будем считать все потоки событий, переводящие СМО из состояния в состояние, пуассоновскими.

Вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой экспоненциального закона распределения:

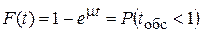, (2)

где μ – интенсивность обслуживания (среднее число событий, происходящих в единицу времени),

. (3)

Не нашли, что искали? Воспользуйтесь поиском: