
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Матрица наблюдений однофакторного дисперсионного комплекса
| Кол-во элементов совокупности (n)-дозы удобрения Кол-во совокупностей (m) | … | J | … | N | ||
| X11 | X12 | … | X1j | … | X1n1 | |
| X21 | X22 | … | X2j | … | X2n2 | |
| … | … | … | … | … | … | … |
| I | Xi1 | Xi2 | … | xij | … | xini |
| … | … | … | … | … | … | |
| m | Xm1 | Xm2 | … | xmj | … | xmnm |
Средние этих выборок обозначим через  b1, b2,…, bi,…, bm. Для проверки гипотезы о равенстве средних нулевую гипотезу запишем как Н0: b1=b2=…=bi=…=bm, альтернативную в виде Н1:b1¹b2¹…¹bi¹…¹bm.
b1, b2,…, bi,…, bm. Для проверки гипотезы о равенстве средних нулевую гипотезу запишем как Н0: b1=b2=…=bi=…=bm, альтернативную в виде Н1:b1¹b2¹…¹bi¹…¹bm.
Гипотеза Н0 проверяется сравнением внутригрупповых и межгрупповых дисперсий по F -критерию. Если расхождение между ними незначительно, то нулевая гипотеза принимается. В противном случае нулевая гипотеза отвергается и делается заключение о том, что различия в средних обусловлены не только случайностями выборок, но и действием исследуемого фактора.
Для изучаемого признака характерно три типа изменчивости:
1. Факториальная (или групповая) изменчивость, характеризующаяся тем, что для каждой из совокупностей имеется своя средняя арифметическая (  ). Разница в медиях зависит, очевидно, от разного действия факторов.
). Разница в медиях зависит, очевидно, от разного действия факторов.
2. Остаточная изменчивость, характеризующаяся различными значениями признака внутри каждой градации. Эти различия не зависят от влияния фактора. Видимо, их причина лежит вне опыта, определяется неучитываемыми в данном анализе факторами.
3. Общая изменчивость, заключающаяся в том, что все наблюдения дисперсионного комплекса отличаются друг от друга (или иногда совпадают).
Мерилом изменчивости признака в выборке служит сумма квадратов отклонений его значений от средней арифметической å(х - 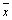 )2. Эта величина, отнесенная к числу наблюдений, дает меру рассеяния, именуемую дисперсией, которая и применяется в дисперсионном анализе.
)2. Эта величина, отнесенная к числу наблюдений, дает меру рассеяния, именуемую дисперсией, которая и применяется в дисперсионном анализе.
1. Мерой факториальной изменчивости будет сумма квадратов отклонений средних значений групп (  ) от общего среднего
) от общего среднего  :
:
S2x= n  . (1.3)
. (1.3)
Эту величину иногда называют рассеиванием по факторам.
2. Мера остаточной изменчивости выразится суммой квадратов отклонений всех наблюдений в данной совокупности от среднего значения совокупности:
S2z=  . (1.4)
. (1.4)
3. Мерой общей изменчивости является сумма квадратов отклонений в дисперсионном комплексе от общего среднего:
S2y=  2. (1.5)
2. (1.5)
Тогда в соответствии с основной идеей дисперсионного анализа можно записать S2y=S2x+S2z или
S2y=  2= n
2= n  +
+  (1.6)
(1.6)
Вычислим факториальную и остаточную дисперсии как меры соответствующих типов изменчивости признака в дисперсионном комплексе:
 (1.7)
(1.7)
В этих формулах фигурируют степени свободы (nх, nz, nу), т.к. дисперсия s2 и есть сумма квадратов отклонений в расчете на одну степень свободы. Число степеней свободы есть количество значений, необходимых для восстановления утерянного. Число степеней свободы для факториальной дисперсии равно числу совокупностей без единицы (m -1), т.к. все группы связаны друг с другом лишь одним общим условием – значением средней арифметической всего дисперсионного комплекса ( 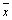 ).Число степеней свободы для остаточной дисперсии равно числу наблюдений в комплексе минус число совокупностей (mn-m), ибо все наблюдения связаны наличием в каждой группе своей средней арифметической (
).Число степеней свободы для остаточной дисперсии равно числу наблюдений в комплексе минус число совокупностей (mn-m), ибо все наблюдения связаны наличием в каждой группе своей средней арифметической ( 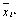 ).Число степеней свободы для вычисления общей дисперсии всего комплекса равно числу наблюдений в комплексе без единицы (mn- 1), ибо все наблюдения связаны только одним общим условием – наличием общей средней (
).Число степеней свободы для вычисления общей дисперсии всего комплекса равно числу наблюдений в комплексе без единицы (mn- 1), ибо все наблюдения связаны только одним общим условием – наличием общей средней ( 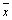 ).
).
Затем необходимо рассчитать доли влияния учтенного и неучтенного факторов как отношения соответствующих сумм квадратов отклонений:
 . (1.9)
. (1.9)
Эти величины представляют собой не что иное, как квадраты корреляционных отношений. В сумме эти показатели должны всегда составлять 1 (100%). Теперь можно ответить на интересующий вопрос: насколько учитываемый фактор ответственен за изменчивость результативного признака и сколько процентов падает на долю неучтенных факторов. Для проверки достоверности полученного вывода необходимо провести проверку по F -критерию. Определяют значение критерия Фишера (F), представляющего собой отношение двух дисперсий – факториальной и остаточной –  , и сравнивают его с табличным в зависимости от числа степеней свободы n1= m -1 и n2= mn-m. Для того чтобы отвергнуть нулевую гипотезу, необходимо, чтобы полученное значение критерия было больше табличного.
, и сравнивают его с табличным в зависимости от числа степеней свободы n1= m -1 и n2= mn-m. Для того чтобы отвергнуть нулевую гипотезу, необходимо, чтобы полученное значение критерия было больше табличного.
Однофакторный дисперсионный анализ удобно представить в виде табл. 2
Таблица 2
Не нашли, что искали? Воспользуйтесь поиском: