Скорость точки при координатном способе задания движения.

Пусть движение точки задано в декартовой системе координат, принятой за неподвижную, т. е. пусть заданы координаты точки как функции времени

, , .

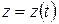Имеем представление радиус-вектора . Так как единичные векторы , , выбранной системы координат постоянны, то на основании формулы (9.11) получаем

.

На рис. 9.11 показано разложение скорости на составляющие по осям координатной системы . Таким образом, проекции скорости , , на координатные оси будут

, , ,

т. е. проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.

Полученные формулы можно переписать в виде

, , . (9.12)

Модуль скорости определяется формулой

, (9.13)

а направление скорости - направляющими косинусами

, ,

.

Если модуль скорости не изменяется с течением времени, то движение называется равномерным.

Движение, заданное в полярных координатах. Пусть даны как функции времени полярный радиус 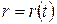и угол 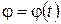, определяющие положение точки. Введем в рассмотрение единичные векторы: , направленный по радиусу-вектору в сторону возрастания 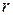, и , повернутый относительно на угол в сторону возрастания угла (рис. 9.13).

Дифференцируя и по времени, представляя их через единичные векторы и , получим

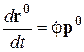(9.15) и . (9.16)

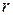Радиус-вектор , определяющий положение точки, может быть представлен в виде (рис. 9.13). При движении точки меняются как модуль, так и направление радиуса-вектора , следовательно, и , и 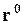являются функциями времени. Тогда, с учётом (9.15), имеем

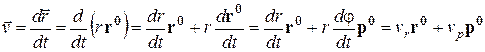, (9.17)

где и называются соответственно радиальной и поперечной скоростями. Модуль скорости находится по формуле .

Не нашли, что искали? Воспользуйтесь поиском: