
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Нахождение ускорения при естественном способе задания движения.

 Рассмотрим пространственную кривую. Из дифференциальной геометрии известно, что через любую точку
Рассмотрим пространственную кривую. Из дифференциальной геометрии известно, что через любую точку 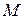 пространственной кривой можно провести касательную (I), нормальную (II) и спрямляющую (III) плоскости (рис. 9.21). На линиях пересечения этих плоскостей определяют единичные вектора касательной
пространственной кривой можно провести касательную (I), нормальную (II) и спрямляющую (III) плоскости (рис. 9.21). На линиях пересечения этих плоскостей определяют единичные вектора касательной 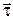 , главной нормали
, главной нормали 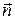 и бинормали
и бинормали 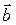 , которые образуют правую систему осей как показано на рис. 9.21. Полученный трехгранник, составленный из соприкасающейся, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Векторы
, которые образуют правую систему осей как показано на рис. 9.21. Полученный трехгранник, составленный из соприкасающейся, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Векторы 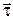 ,
, 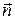 и
и 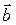 являются единичными векторами осей естественного трехгранника.
являются единичными векторами осей естественного трехгранника.
Обозначим через 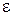 величину угла между вектором
величину угла между вектором 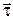 , проведенным в точке
, проведенным в точке 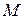 , и вектором
, и вектором 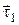 , проведённым в точке
, проведённым в точке 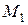 , близкой к точке
, близкой к точке 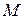 . Этот угол называется углом смежности (рис. 9.22).
. Этот угол называется углом смежности (рис. 9.22).


 Кривизной кривой в точке
Кривизной кривой в точке 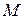 называют предел отношения угла смежности
называют предел отношения угла смежности 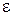 к абсолютному значению длины дуги
к абсолютному значению длины дуги 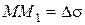 , т. е.
, т. е. 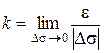 .
.
Радиусом кривизны кривой в точке 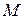 называется величина, обратная кривизне
называется величина, обратная кривизне 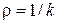 . Так кривизна прямой равна нулю, а её радиус кривизны равен бесконечности. Кривизна окружности во всех ее точках одинакова и равна обратной величине радиуса
. Так кривизна прямой равна нулю, а её радиус кривизны равен бесконечности. Кривизна окружности во всех ее точках одинакова и равна обратной величине радиуса 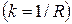 . Радиус кривизны равен радиусу окружности
. Радиус кривизны равен радиусу окружности 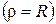 .
.
Учитывая представление вектора скорости (9.20) 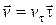 , на основании определения ускорения (9.21), имеем
, на основании определения ускорения (9.21), имеем
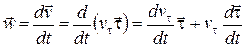 .
.
Найдем производную вектора 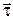 :
:
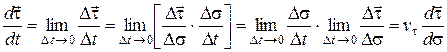 .
.
Вектор 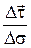 всегда направлен в сторону вогнутости траектории (см. рис. 9.22) и лежит в плоскости, проходящей через точку
всегда направлен в сторону вогнутости траектории (см. рис. 9.22) и лежит в плоскости, проходящей через точку 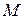 и векторы
и векторы 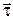 и
и 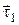 (плоскость
(плоскость 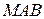 ). Следовательно, вектор
). Следовательно, вектор 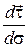 лежит в соприкасающейся плоскости, так как при
лежит в соприкасающейся плоскости, так как при 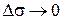 (
( ) плоскость
) плоскость 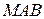 совпадает с соприкасающейся плоскостью к траектории в точке
совпадает с соприкасающейся плоскостью к траектории в точке 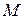 .
.
Дифференцируя тождество 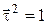 по
по 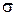 , получим
, получим 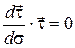 . То есть скалярное произведение
. То есть скалярное произведение 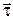 на
на 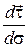 равно нулю, а это значит, что вектор
равно нулю, а это значит, что вектор 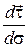 перпендикулярен
перпендикулярен 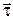 . Таким образом, этот вектор лежит в соприкасающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен
. Таким образом, этот вектор лежит в соприкасающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен 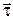 . Следовательно, он направлен по главной нормали к центру кривизны.
. Следовательно, он направлен по главной нормали к центру кривизны.
Определим теперь модуль этого вектора. Из равнобедренного треугольника 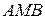 (рис. 9.22)
(рис. 9.22) 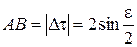 . Тогда
. Тогда
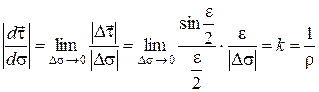 .
.
Учитывая, что 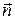 есть единичный вектор главной нормали, будем иметь
есть единичный вектор главной нормали, будем иметь 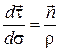 . Значит,
. Значит, 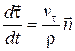 и, следовательно,
и, следовательно, 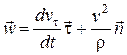 , так как
, так как 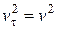 .
.
Из этой формулы следует, что вектор ускорения лежит в соприкасающейся плоскости.
Составляющие ускорения по направлениям 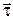 и
и 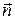 соответственно равны
соответственно равны
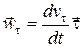 ,
, 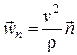
и называются касательным (тангенциальным) ускорением и нормальным ускорением. Касательное ускорение характеризует изменение модуля скорости, а нормальное ускорение характеризует изменение скорости по направлению.
Модуль вектора ускорения равен  .
.
Если 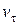 и
и  одного знака, то модуль скорости точки возрастает и движение в этом случае называется ускоренным. Если же
одного знака, то модуль скорости точки возрастает и движение в этом случае называется ускоренным. Если же 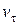 и
и  разных знаков, то модуль скорости точки убывает и движение будет замедленным. При
разных знаков, то модуль скорости точки убывает и движение будет замедленным. При 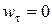 модуль скорости остается постоянным - движение равномерное.
модуль скорости остается постоянным - движение равномерное.
Не нашли, что искали? Воспользуйтесь поиском: