
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Скорость точки при естественном способе задания движения.
Пусть точка 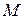 движется по какой-либо кривой. За промежуток времени
движется по какой-либо кривой. За промежуток времени 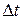 точка переместится по кривой из положения
точка переместится по кривой из положения 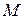 в положение
в положение 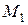 по дуге
по дуге 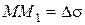 . По определению скорости имеем
. По определению скорости имеем
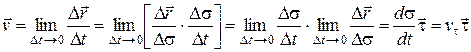 , (9.20)
, (9.20)
где 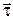 - единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги. Так как проходимый точкой путь всегда положителен, то элемент пути
- единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги. Так как проходимый точкой путь всегда положителен, то элемент пути 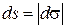 и, следовательно, модуль скорости можно определить по формуле
и, следовательно, модуль скорости можно определить по формуле 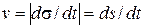 .
.
 Ускорение точки. Предположим, что в момент времени
Ускорение точки. Предположим, что в момент времени  скорость точки равна
скорость точки равна  , а в момент времени
, а в момент времени 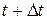 будет
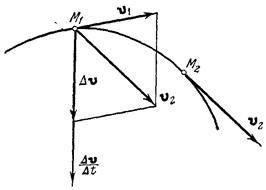
будет  (рис. 9.18). Изменение вектора скорости за промежуток времени
(рис. 9.18). Изменение вектора скорости за промежуток времени 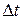 найдем как разность векторов
найдем как разность векторов 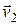 и
и 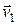 , если параллельно перенесем вектор
, если параллельно перенесем вектор 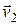 в точку
в точку 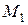 (рис. 9.18). Вектор
(рис. 9.18). Вектор
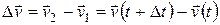
представляет собой приращение вектора скорости за промежуток времени 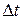 .
.
 Отношение вектора
Отношение вектора 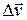 к промежутку времени
к промежутку времени 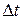 называется средним ускорением точки за промежуток времени
называется средним ускорением точки за промежуток времени 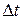 :
: 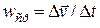 .
.
Ускорением 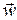 точки в данный момент времени называется предел отношения приращения скорости
точки в данный момент времени называется предел отношения приращения скорости 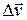 к приращению времени
к приращению времени 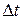 при условии, что последнее стремится к нулю, т. е.
при условии, что последнее стремится к нулю, т. е.
 , (9.21)
, (9.21)
так как 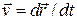 . Можно также пользоваться записью:
. Можно также пользоваться записью:  .
.
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса-вектора точки.
Годографом скорости называется кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости проводится из одной и той же точки.
Очевидно, что скорость точки, вычерчивающей годограф скорости, будет равна 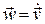 , т. е. ускорению точки при ее движении по траектории. Размерность ускорения
, т. е. ускорению точки при ее движении по траектории. Размерность ускорения 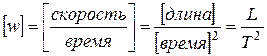 , т.е.
, т.е. 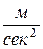 ,
, 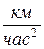 и т. д.
и т. д.
Нахождение ускорения при координатном способе задания движения. Пусть движение точки задано в прямоугольной системе координат:
 ,
,  ,
, 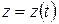 .
.
Так как вектор скорости точки можно представить в виде 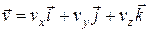 , то на основании (9.21) будем иметь
, то на основании (9.21) будем иметь
 ,
,
т. е. проекция ускорения точки на какую-либо координатную ось равна первой производной по времени от соответствующей проекции скорости точки.
Можно записать также, что  ,
, 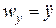 ,
,  . Следовательно, проекция ускорения точки на какую-либо координатную ось равна второй производной по времени от соответствующей координаты. Модуль ускорения определяется по формуле
. Следовательно, проекция ускорения точки на какую-либо координатную ось равна второй производной по времени от соответствующей координаты. Модуль ускорения определяется по формуле 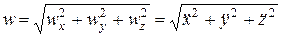 .
.
Зная проекции ускорения и его модуль, легко находим направляющие косинусы вектора ускорения:
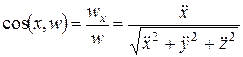 ,
,  ,
,
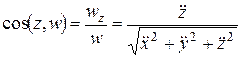 .
.
Движение, заданное в полярных координатах. Пусть координаты точки заданы как функции времени: 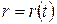 и
и 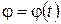 . Согласно (9.17) имеем
. Согласно (9.17) имеем
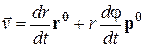 .
.
Тогда по определению (9.21) получим
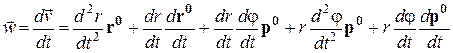 .
.
Так как на основании (9.15) и (9.16) 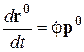 и
и  , то
, то
 .
.
Отсюда находим проекции ускорения на радиальное и поперечное направления
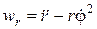 ,
,  (9.26)
(9.26)
Модуль и направление вектора ускорения определяются по формулам
 ,
,  ,
,  .
.
Не нашли, что искали? Воспользуйтесь поиском: