Операции над матрицами.

1. Умножение матрицы на число. Произведением матрицы А на число называется матрица , элементы которой . Например, если .

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

1. Сложение матриц. Суммой двух матриц А и В одинакового размера называется матрица С=А+В, элементы которой ; (т.е. матрицы складываются поэлементно).
2. Вычитание матриц. Разность двух матриц одинакового размера определяется через операции А-В=А+(-1)В.

Замечание. Операции сложения и умножения на число называются линейными операциями.

1. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц называется такая матрица , каждый элемент которой равен сумме произведений элементов -той строки матрицы А на соответствующие элементы 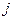-того столбца матрицы В. ; .

Пример. Вычислить произведение матриц .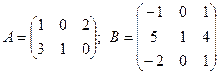

Решение. .

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами:

А+В=В+А; (А+В)С=АС+ВС;

(А+В)+С=А+(С+В); (АВ)= ( А)В=А( В);

(А+В)= А+ В; А(ВС)=(АВ)С.

А(В+С)=АВ+АС;

Однако имеются и специфические свойства матриц. Так операция умножения матриц имеет отличия от умножения чисел:

а) Если произведение матриц АВ существует, то после перестановки матриц местами произведение матриц ВА может и не существовать. Так в рассмотренном выше примере произведение ВА не существует, т.к. число столбцов первой матрицы (В) не равно числу строк второй матрицы (А).

б) Если даже произведения АВ и ВА существуют, то они могут быть матрицами разных размеров.

в) В случае, когда оба произведения существуют и это матрицы одного размера (это возможно, если перемножались квадратные матрицы одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е. .

В частном случае коммутативным законом обладает произведение любой квадратной матрицы А п -го порядка на единичную матрицу Е того же порядка, причем это произведение равно А: .

Т.о. единичная матрица играет при умножении матриц такую же роль, что и число 1 при умножении чисел.

г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что АВ=0 не следует, что А=0 или В=0. Например, .

5. Возведение в степень. Целой положительной степенью квадратной матрицы А называется произведение т матриц А, т.е. . Нетрудно показать, что:

.

6. Транспонирование матрицы – переход от матрицы к матрице , в которой строки и столбца поменялись местами с сохранением порядка.

. Обозначают транспонированную матрицу также символом .

Из определения следует, что, если матрица А имеетразмер , то транспонированная матрица имеет размер .

Не нашли, что искали? Воспользуйтесь поиском: