Метод обратной матрицы

Систему линейных уравнений можно записать в матричной форме, для этого введем обозначения:

- матрица коэффициентов при неизвестных;

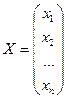- матрица-столбец переменных; - матрица-столбец свободных членов. Теперь систему можно записать в виде: .

Матрица называется расширенной матрицей системы уравнений.

Пусть число уравнений системы равно числу переменных, т.е. 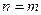. Тогда матрица системы является квадратной, а её определитель является определителем системы.

Для получения решения системы при предположим, что квадратная матрица системы невырожденная, т.е. ее определитель . В этом случае существует обратная матрица .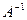

Умножая слева обе части матричного равенства на матрицу 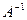, получим . Т.к. 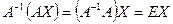, то решением системы методом обратной матрицы будет матрица–столбец

Не нашли, что искали? Воспользуйтесь поиском: