Решение систем линейных уравнений методом Гаусса.

Нахождение обратной матрицы через алгебраические дополнения - трудоемкий вычислительный процесс, поэтому при решении системы линейных уравнений воспользуемся численным методом, который поз­воляет с помощью элементарных преобра­зо­ваний за конечное число шагов найти решение (если оно сущест­ву­ет) и при необходимости по­лучить обратную матрицу. Этот метод называется методом полного исключения неизвестных или мето­дом Гаусса.

Пусть дана система уравнений, запишем ее расширенной матрицей

Идея метода состоит в том, чтобы с помощью элементарных преобразований свести расширенную матрицу системы к виду .

Преобразование системы состоит из ряда последовательных шагов. Условимся, что перед выполнением очередного шага в таблице вычеркиваются все строки, состоящие из одних нулей, т.е. вычеркиваются все тривиальные уравнения.

Пример. Решим систему методом Гаусса.

Начальная расширенная матрица имеет вид .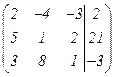

Приведем ее к диагональному виду.

1-й шаг. Получим в первой строке единицу, для этого разделим первую строку матрицы на 2.

.

2-й шаг. «Обнулим» первый столбец, т.е. получим нули на месте элементов . Для этого 1-ю строку оставляем без изменения. Вместо 2-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-5), складываем ее со 2-й строкой, тогда новые числа, стоящие во 2-й строке расширенной матрицы, будут следующие:

Вместо 3-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-3) и складываем ее с 3-й строкой, тогда

Расширенная матрица примет вид .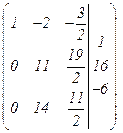

В результате 1-й столбец 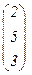преобразовался в .

3-й шаг. Получим 1 во второй строке, для этого делим вторую строку на 11.

.

4-й шаг. «Обнулим» второй столбец: (получим нули на месте элементов . Для этого 2-ю строку оставляем без изменения. Вместо 1-й строки записываем следующую ее комбинацию со 2-й: 2-ю строку умножаем на 2 и складываем ее с 1-й строкой, тогда

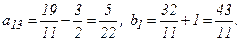
Вместо 3-й строки записываем ее комбинацию со 2-й: 2-ю строку умножаем на

(-14) и складываем ее с 3-й строкой, тогда

.

В результате 1-й столбец матрицы не изменился, а 2-й превратился в .

5-й шаг. Получим 1 в третьей строке. Делим 3-ю строку на :

.

6-й шаг. «Обнулим» третий столбец, для чего 3-ю строку оставляем без изменения. Вместо 1-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на и складываем ее с 1-й строкой, тогда

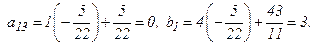
Вместо 2-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на и складываем ее с 2-й строкой, тогда

.

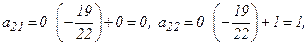
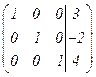В результате 5-го и 6-го шагов 3-й столбец принял вид .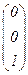

Таким образом, решение системы следующее:

Проверка:

Не нашли, что искали? Воспользуйтесь поиском: