Определители квадратных матриц.

· Определителем квадратной матрицы А п-го порядка или определителем п-го порядка называется число, равное алгебраической сумме п! членов, каждый из которых является произведением п элементов матрицы, взятых по одному из каждой строки и каждого столбца с определенными знаками. Определитель обозначается или .

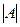Определитель второго порядка есть число, выраженное следующим образом: . Например .

Определитель третьего порядка вычисляется по правилу треугольников (правило Саррюса): .

Пример. .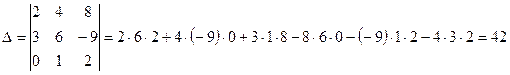

Замечание. Практически определители третьего порядка, как и более высоких порядков, вычисляются с использованием свойств определителей.

Свойства определителей п-го порядка.

1. Величина определителя не изменится, если каждую строку (столбец) заменить столбцом (строкой) с тем же номером – транспонировать.

2. Если одна из строк (столбец) определителя состоит из нулей, то величина определителя равна нулю.

3. Если в определителе поменять местами две строки (столбца), то абсолютная величина определителя не изменится, а знак поменяется на противоположный.

4. Определитель, содержащий две одинаковые строки (столбца), равен нулю.

5. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.

· Минором некоторого элемента определителя п -го порядка называется определитель (п -1)-го порядка, полученный из исходного вычеркиванием той строки и того столбца, на пересечении которых находится выбранный элемент. Обозначение: .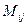

· Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком . Обозначение: Т.о. = .

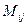6. Определитель квадратной матрицы равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения (теорема разложения).

7. Если каждый элемент -той строки представляет собой сумму k слагаемых, то определитель представляется в виде суммы k определителей, у которых все строки, кроме -той строки, такие же как в исходном определителе, а -тая строка в первом определителе состоит из первых слагаемых, во втором – из вторых и т.д. То же верно и для столбцов.

8. Определитель не изменится, если к одной из строк (столбцов) прибавить другую строку (столбец), умноженную на число .

Следствие. Если к строке (столбцу) определителя прибавить линейную комбинацию других ее строк (столбцов), то определитель не изменится.

9. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.

Замечание. Определитель треугольной матрицы также равен произведению элементов, стоящих на главной диагонали.

Перечисленные свойства определителей позволяют значительно упростить их вычисление, что особенно важно для определителей высоких порядков. При этом целесообразно так преобразовать исходную матрицу, чтобы преобразованная матрица имела строку или столбец, содержащую как можно больше нулей («обнуление» строк или столбцов).

Примеры. Вычислим еще раз определитель , приведенный в предыдущем примере, используя свойства определителей.

Решение: Заметим, что в первой строке имеется общий множитель - 2, а во второй - общий множитель 3, вынесем их за знак определителя (по свойству 5). Далее разложим определитель, например, по первому столбцу, используя свойство 6 (теорему разложения).

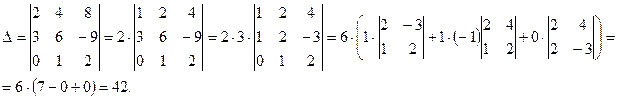
Наиболее эффективен метод приведения определителя к диагональному или к треугольному виду. Для вычисления определителя матрицы достаточно выполнить такое преобразование матрицы, которое не изменит определителя и позволит превратить матрицу в диагональную.

В заключении заметим, что если определитель квадратной матрицы равен нулю , то матрица называется вырожденной (или особенной), в противном случае – невырожденной.

Обратная матрица.

Для любого действительного числа существует обратное число такое, что . Для квадратных матриц вводится аналогичное понятие.

· Определение. Матрица 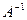называется обратной по отношению к квадратной матрице , если при умножении этой матрицы на обратную, как справа, так и слева получается единичная матрица .

Из определения следует, что только квадратная матрица имеет обратную; при этом обратная матрица также является квадратной того же порядка. Однако не каждая квадратная матрица имеет обратную.

Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 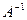существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная .

Алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы. Если , то матрица - вырожденная и не имеет обратной матрицы.
2. Находим матрицу - транспонированную к .
3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них матрицу, заменяя каждый элемент матрицы его алгебраическим дополнением. Такая матрица называется присоединенной (или союзной), обозначим ее .
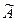4. Вычисляем обратную матрицу по формуле .
5. Проверяем правильность вычисления обратной матрицы 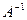, исходя из её определения: .

Пример 1. Найти матрицу, обратную данной .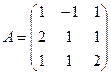

1. Найдем определитель матрицы 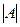разложением по первой строке 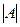= , следовательно, матрица А невырожденная и обратная матрица существует.
2. Находим матрицу , транспонированную к А:
3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу:

.

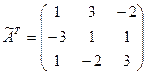1. Вычисляем обратную матрицу .
2. Проверяем правильность вычисления обратной матрицы по формулам: (выполнить самостоятельно).

Не нашли, что искали? Воспользуйтесь поиском: