Конкретизация понятия алгоритма

Задачу алгоритмической разрешимости можно сформулировать следующим образом: задача алгоритмически разрешима, если для нее можно построить рекурсивную функцию (машину Тьюринга, λ – нотацию, алгорифм Маркова).

Машины Тьюринга

Машина Тьюринга (МТ) – это математическая модель идеализированного вычисляемого устройства. Для построения МТ надо задать:

1. Конечный алфавит , где 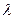- пустой символ.

2. Конечное множество внутренних состояний .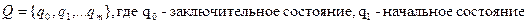

МТ представляет собой

· Бесконечную ленту, разделенную на ячейки. В каждый момент времени в ячейке записана буква . В процессе работы в ячейку может быть записан другой символ

· По ячейкам передвигается управляющее устройство (УУ). В каждый момент времени оно находится напротив какой-то ячейки и имеет некоторое состояние .

Машина действует дискретно, т. е. в определенные моменты времени.

Если в какой-то момент времени УУ воспринимает ячейку, содержащую символ и МТ находится в состоянии , то МТ может совершить следующие действия:

1. Стереть символ и записать на его место символ .

2. Переместиться в ячейку слева (Л).

3. Переместиться в ячейку справа (П).

4. Остаться на месте (С).

Эти действия называются программой.

Таким образом, М=<A,Q, П>.

Программу МТ можно представить в виде последовательности команд вида: ,

где D={Л, П, С}. (Л- переход влево, П – переход вправо, С – остаться на месте).

Программу также можно представить в виде таблицы:

	q1	q2	….	qn
a1
a2
….
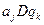
am

Пример. МТ добавляет к слову единицу.

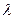
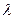
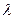
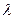
Программа:

(Если в воспринимаемой ячейке символ 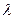, и МТ находится в состоянии q_1, то состояние не меняется, символ не меняется, УУ сдвигается вправо).

(Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q_1, то это значит, что УУ находится на начале слова, состояние меняется на q₂, символ не меняется, УУ сдвигается вправо).

(Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q_2, то это значит, что УУ передвигается по слову, состояние не меняется, символ не меняется, УУ сдвигается вправо).

(Если в воспринимаемой ячейке символ 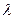, и МТ находится в состоянии q_2, то это значит, что УУ дошло до конца слова, состояние меняется на заключительное, символ меняется на 1, УУ останавливается).

В виде таблицы эту программу можно записать следующим образом:

	q1	q2

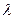
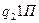
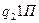
Конфигурация МТ (машинное слово) – это слово вида , где

p₁ – слово в алфавите МТ (может быть пустое),

q_s – внутреннее состояние М,

a_i – воспринимаемый символ,

p₂ – слово в алфавите МТ.

МТ переводит конфигурацию в конфигурацию (), если имеет вид , имеет вид , - одна из команд МТ.

Для рассмотренного выше примера:

1. Команда переводит МТ из конфигурации в конфигурацию

2. Команда переводит МТ из конфигурации в конфигурацию

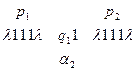
и т. д.

МТ останавливается при конфигурации , если не существует такой конфигурации , что (т. е. входит в , а среди команд МТ нет такой, которая бы начиналась с ).

Тезис Тьюринга: Любой интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.

Не нашли, что искали? Воспользуйтесь поиском: