Нормальные алгорифмы Маркова

Алгоритмическая система Маркова строится по тем же принципам, что и МТ, но носит более простой и интуитивно понятный характер.

Нормальные алгорифмы Маркова (НАМ) представляются нормальной схемой подстановок, которая состоит из совокупности подстановок, расположенных в определенном порядке.

Пусть Х – некоторый конечный алфавит, F(X) – слова алфавита, - пустое слово. Если , то выражения и называются формулами подстановки в алфавите Х:

- простая подстановка;

- окончательная подстановка.

Символы → и. не принадлежат Х.

Слова p и q могут быть пустыми.

Строка R входит в строку L, если L имеет вид L₁RL₂. Подстановка применима к слову, если строка соответствующая левой части подстановки входит в слово. Применение заключается в замене в преобразующем слове левой строки – правой:

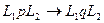
Механизм работы НАМ:

Дано преобразуемое слово – цепочка символов фиксированного алфавита и нормальная схема подстановок, содержащая фиксированную последовательность простых и заключительных подстановок.

1) Слово всегда просматривается слева направо. Схема подстановок просматривается, начиная с первой подстановки, и, если подстановку можно применить, то она применяется к самому левому вхождению этой строки в преобразуемое слово.

2) Работа алгоритма заканчивается если:

· ни одна из подстановок не применима,

· использована заключительная подстановка.

Может возникнуть ситуация, когда процесс не закончится никогда. В этом случае считают, что алгоритм не применим к слову.

Пример.

Х={x,y,z};

Нормальная схема подстановок:

xx ® y

xy ® x

yzy ® x

zz ®. z

yy ® x

Преобразуемое слово:

xx xyyyzzz →y xy yyzzz→y xy yzzz →y xy zzz→yx zz z→yxzz

Пример.

X={А,Б,В,Г,…,Я};

Нормальная схема подстановок:

Х®К

М®Р

КА®ЛОН

РУ®.С

Преобразуемое слово:

МУ Х А® М УКА®РУ КА ® РУ ЛОН®СЛОН

Пример 9:

X={a,b};

Нормальная схема подстановок:

a→.e

b→b

Преобразуемое слово:

bbbbbb - схема не применима.

Преобразуемое слово:

abab →bab

Пример.

Х={х,у,х^-1,у^-1};

Нормальная схема подстановок:

х х^-1→е

х^-1х→е

у у^-1→е

у^-1у→е

Преобразуемое слово:

ххух уу ^-1х^-1ух→ хху хх ^-1ух→ ххуух

Пример 10:

Х={x₁, …,x_n};

Нормальная схема подстановок:

x₁→e

x₂→e

…

x_n→e

Преобразуемое слово переписывается в пустое.

Пусть R и Q нормальные алгорифмы над алфавитом Х и pÎF(x). Запись означает, что или оба алгорифма R и Q не применимы к слову p, или оба применимы и .

Два алгорифма R и Q называют эквивалентными относительно алфавита Х, если каждый раз, когда pÎF(x) и хотя бы одно из слов R(p) или Q(p) определено и тоже принадлежит F(x).

Если для всех pÎF(x) , то R и Q называются полностью эквивалентными.

Пусть X={1}, а . Тогда всякое натуральное число n можно записать в виде слова в алфавите :

Поставим в соответствие вектору (n₁, n₂, …n_k), где n₁, n₂, …n_k – натуральные числа, слово в алфавите вида , которое обозначим . Например, вектору соответствует слово 11111*1*111.

Пусть f: N^k→N – некоторая частичная функция и R_f обозначает алгорифм в алфавите такой, что

тогда и только тогда, когда хотя бы одна из частей равенства определена. При этом считается, что алгорифм R_f не применим к словам отличным от вида .

Функция f называется частично определимой по Маркову, если существует нормальный алгорифм Q над полностью эквивалентный R_f над . Если функция определена полностью, то ее называют просто вычислимой по Маркову.

Теорема: Простейшие функции O(x)=0, S(x)=x+1 и I_m(x₁,x₂,…,x_n)=x_m вычислимы по Маркову.

Доказательство сводится к построению соответствующих алгорифмов.

1.Функцию O(x)=0 реализует следующий алгорифм R₀:

={1,*}, ;

Нормальная схема подстановок:

*→* (1)

α11→ α1 (2)

α1→.1 (3)

е→ α (4)

Преобразуемое слово:

р=111…11.

Тогда по формуле (4) получаем р= α 11…11.

Применим формулу (2) и получим: р= α 11 …11→ α 1 …11→ α 1.

Применяем формулу (3) и получаем α 1 →1.

Так как 1 – это в алфавите Х, то R₀ и является искомым алгоритмом.

2. Функцию S(x)=x+1 реализует следующий алгорифм R_s:

={1,*}, ;

Нормальная схема подстановок:

*→* (1)

α1→.11 (2)

е→ α (3)

Преобразуемое слово:

р=111…11.

Тогда по формуле (3) получаем р= α 1 1…11 (n единиц).

Применим формулу (2) и получим: р= 111 …11 (n+1 единица). Так как всякое натуральное число n можно записать в виде слова в алфавите :

, то мы реализовали алгоритм R_S(n)=n+1.

Этот алгоритм применим только к тем словам, которые являются натуральными числами.

3. Алгорифм R_I имеет более сложную структуру, с ним можно ознакомиться самостоятельно в учебнике «Лекции по дискретной математике», авторы: Капитонова Ю.В. и др.

Теорема: Всякая частично рекурсивная функция частично рекурсивна по Маркову.

Обратная теорема: всякая частично вычислимая по Маркову функция является частично рекурсивной.

Не нашли, что искали? Воспользуйтесь поиском: