Рекурсивные функции

Будем рассматривать только числовые функции, т. е. функции, аргументы и значения которых принадлежат множеству натуральных чисел N (N=0,1,2,…).

Если область определения функции совпадает с множеством 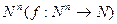, то функция называется всюду определенной, иначе – частично определенной.

Пример:

f(x,y)=x+y – всюду определенная функция,

f(x,y)=x-y – частично определенная функция, т. к. она определена только для .

Рекурсивное определение функции – это такое определение, при котором значение функции для данных аргументов определяется значениями той же функции для более простых аргументов или значениями более простых функций.

Примеры:

1. Числа Фибоначчи (1, 1, 2, 3, 5, 8, …) это последовательность чисел f(n), где f(0)=1, f(1)=1, f(n+2)=f(n)+f(n+1).

2. Факториал (n!=1*2*3*…*n) f(0)=1, f(n+1)=f(n)*(n+1).

Рекурсивные функции строятся на основе трех примитивных (заведомо однозначно понимаемых и реализуемых) функций. Их также называют простейшими.

1. S(x)=x+1 – функция следования.

Примеры: S(0)=1, S(1)=2, S(-5) – не определена.

2. О(х)=0 – нуль-функция;

Примеры: О(0)=0, О(1)=0, О(-5) – не определена.

3. I_m(x₁,x₂,…,x_n)=x_m, (m=1,2,…n) – функция проектирования (выбора аргумента).

Пример: I₂(1,2,3,4,…n)=2.

С примитивными функциями можно производить различные манипуляции, используя три оператора: суперпозиции, примитивной рекурсии и минимизации.

1. Оператор суперпозиции (подстановки).

Пусть f – m-местная функция, g₁,…g_m – n-местные операции на множестве N. Оператор суперпозиции S ставит в соответствие операциям f и g₁,…g_m n-местную функцию h.

Примеры:

1) Используя оператор суперпозиции, можно получить любую константу.

S(O(x))=0+1=1

S(S(O(x)))=0+1+1=0+2=2

S(S…(O(x))…)=0+n, где число вложений функций следования n.

2) Используя оператор суперпозиции, можно выполнить сдвиг на константу n.

S(x)=x+1

S(S(x))=x+1+1=x+2

S(S…(S(x))…)=x+n.

2. Оператор примитивной рекурсии

Оператор R каждой (n+2)-местной операции f и n-местной операции g ставит в соответствие (n+1)-местную операцию h=R(f,g), удовлетворяющую следующей схеме:

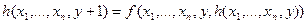
Для n=0 схема примитивной рекурсии имеет вид:

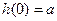, где а – константа,

Пример: Вычисление факториала с использованием оператора примитивной рекурсии будет выглядеть следующим образом.

Схема примитивной рекурсии образует процесс построения функции h, при котором на нулевом шаге используется функция g, а на каждом последующем шаге значение функции f от аргументов , номера y предыдущего шага и значения функции h, вычисленного на предыдущем шаге.

Функция называется примитивно-рекурсивной (ПРФ), если она может быть получена из простейших функций с помощью оператора суперпозиции или оператора примитивной рекурсии.

Примеры:

1) 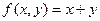- примитивно-рекурсивная функция.

Схема примитивной рекурсии:

2) - примитивно-рекурсивная функция.

3. Оператор минимизации ( -оператор)

, где y – выделенная переменная.

Работу -оператора можно описать следующим образом. Выделяется переменная y, затем фиксируются остальные переменные . Значение у последовательно увеличивается, начиная с 0. Значением -оператора будет то значение у, при котором функция впервые обратилась в 0.

Если функция не обратилась в 0 или принимает отрицательное значение, то значение -оператора считается неопределенным.

Пример: g(x,y)=x-y+3;

Зафиксируем х=1 и будем менять y.

, т. к. 1-1+3=3

, т. к. 1-2+3=2

, т. к. 1-3+3=1

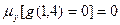, т. к. 1-1+3=0

Следовательно, .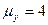

Функция f(x₁,x₂,…,x_n) называется частично рекурсивной (ЧРФ), если она может быть получена из простейших функций с помощью конечного числа применений операций суперпозиции, примитивной рекурсии и минимизации.

Пример.

f(x,y)=x-y - частична, т. к. она не определена, если x<y. Чтобы сделать эту функцию полностью определенной на множестве натуральных чисел N, рассматривают усеченную разность.

Свойства усеченной разности.

1)

2)

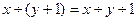
3)

• Докажем, что - примитивно-рекурсивная функция.

Функция примитивно рекурсивна, т. к. по схеме примитивной рекурсии:

1) При х=0 .

2)

Т. о. ее можно получить из простейших функций О(х) и I_m(x₁,…x_n) с помощью оператора простейшей рекурсии R.

• Докажем, что 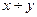- примитивно-рекурсивная функция.

По схеме примитивной рекурсии

1)

2)

Т. о. функцию 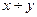можно получить с помощью операции примитивной рекурсии из функций и h(x,y,z)= .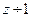

• Функция также является примитивно-рекурсивной
• - примитивно-рекурсивная функция.
• Функцию f(x,y)=x-y можно получить с помощью оператора минимизации:

.

Следовательно, функция f(x,y)=x-y является частично-рекурсивной функцией.

Всюду определенная частично-рекурсивная функция является общерекурсивной (ОРФ).

Для алгоритмических проблем типичной является ситуация, когда требуется найти алгоритм для вычисления числовой функции f(x₁,…x_n). Числовые функции, значения которых можно вычислить с помощью некоторого алгоритма, называются вычислимыми функциями. Это понятие интуитивно, т. к. интуитивно понятие алгоритма.

Функция f(x₁,…x_n) эффективно вычислима, если существует алгоритм, с помощью которого можно найти f(k₁,…k_n), если известны k₁,…k_n.

Тезис Черча. Всякая эффективно вычислимая функция является частично-рекурсивной функцией.

В формулировку тезиса Черча входит понятие эффективной вычислимости. Поэтому его нельзя ни доказать, ни опровергнуть в математическом смысле.

Частичная рекурсивность – это уточнение понятия вычислимой функции. С его помощью можно уточнять или опровергать вычислимость.

Любая частично-рекурсивная функция является вычислимой по Тьюрингу и наоборот.

Не нашли, что искали? Воспользуйтесь поиском: