ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЭЛЕКТРОТЕХНИКАНЫҢ НЕГІЗГІ ЗАҢДАРЫ
ОМ ЗАҢЫ - кернеудің түсуі кедергі арқылы ететін токтың көбейтіндісіне тең.
U=IR
I=U/R
R=U/I
ДЖОУЛЬ-ЛЕНЦ ЗАҢЫ- электр тоғының жылу әрекетін сипаттайтын заң. Бұл заңға сәйкес, өткізгіште тұрақты тоқ өткенде бөлінетін жылу мөлшері Q (джоуль) тоқ күшінен I (ампер), өткізгіш кедергісінен R (ом) және оның өтетін уақытынан t (секунд) тәуелді:
Q = I2Rt
КИРХГОФ ЗАҢДАРЫ
Бірінші заңы тізбектің түйініне бағыталған тоқтардың қосындысы (оң) мен түйінінен шығатын тоқтардың қосындысы (теріс) арасындағы байланысты анықтайды, яғни ∑I = 0.
Сурет 1 - Тоқ түйіні
| Тізбектің кез келген нүктелерінде (түйінде) топтасатын тоқтардың алгебралық қосындысы нөлге тең. Мысалы, мына түйін үшін (сурет 1) былай жазуға болады: I1 + I2 + I3= I5 + I4 немесе I1 + I2 + I3 – I4 – I5 = 0. |
Екінші заңы электр қозгаушы күштердің қосындысы мен электр тізбектің тұйык контурының кедергілеріне түсетін кернеулерінің қосындысы арасындағы байланысты анықтайды ±∑U = ±∑E. Контурды айналудың еркін бағытымен сәйкес келетін тоқтар оң деп, ал сәйкеспейтіндері - теріс деп есептеледі.
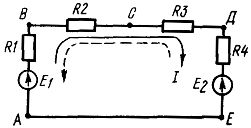Сурет 2 - Ток контуры
| Сызба үшін (сурет 2) Кирхгофтың 2 заңы келесідей: (R1+R2+R3+R4)I = E1 – E2 |
ТОЛЫҚ ТОҚ ЗАҢЫ электромагнитті өрістің негізгі заңдарының бірі. Ол беттік арқылы өтетін магнитті күштер мен тоқ шамасының арасындағы байланысты айқындайды. Толық тоқ дегеніміз тұйық контурмен шектелген беттікті тесіп өтетін тоқтардың алгебралық қосындысын білдіреді.
Контур бойындағы магниттеуші күш осы контурмен шектелген беттік арқылы өтетін тоққа тең. Жалпы жағдайда магнитті сызықтың әр түрлі участоктарындағы өрістің кернеулігі әр түрлі мәнге ие болуы мүмкін, онда магниттеуші күш әр сызыктың магниттеуші күштерінің косындысына тең.
ЛЕНЦ ЗАҢЫ - электромагнитті индукцияның барлык жағдайын қамтитын негізгі ереже және индукцияның пайда болатын ЭҚК бағытын аныктайды.
Ленц заңына сәйкес бұл бағыт барлық жағдайларда ЭҚК- н пайда болған тоқ индукцияның ЭҚК пайда болуы өзгерісіне қарсыласады деп алынады. Бұл заң электромагнитті индукцияға энергияның сақталу заңын сапалы қалыптасуы заңы болып табылады.
ЭЛЕКТРОМАГНИТТІК ИНДУКЦИЯ ЗАҢЫ, Фарадей заңы - магнитті және электр құбылыстары арасындағы байланысты айкындайтын заң. Контурдағы электромагнитті индукцияның ЭҚК сандық түрде тең және осы контурмен шектелген беттік арқылы өтетін магнит ағынының жылдамдығының таңбасы бойынша қарама - қарсы. Өрістің ЭҚК шамасы магнит ағынының өзгеру жылдамдығына тәуелді.
ЭЛЕКТР ТІЗБЕГІНІҢ ЭЛЕМЕНТТЕРІ
Активті элементтер электр энергия көздері болып табылады.
Пассивті элементтер - электр энергия көздері болып табылмайтын элементтер. Олар активті (диссипативті) және реактивті деп бөлінеді.
Реактивті элементтер - электр энергиясын жинақтай алатын, оны энергия алынған көзге, не болмаса басқа элементке бере алады. Бұл элемент электр энергияны жылу энергиясына айналдырмайды. Мұндай элементтер индуктивтілік катушкасы мен конденсатор болып табылады.
Электр тізбек дегеніміз электр энергия көзінің әсерінен элементтерде электр тоғы өтетін электр элементтерінің косындысы.
Тармақ - ең болмағанда бір элементке ие және бірдей тоқ өтетін екі түйін арасында орналасатын тізбек участогы.
Түйін - үш немесе одан да көп өткізгіштердің (тармақтардың) қосылысы. Контур - электр тізбегінің тұйық бөлігі.
Электр тізбектін классификациясы келесі белгілер бойынша анықталады:
- тізбекте электр энергия көзінің болуы немесе болмауы;
- тізбекте активті элементтердің болуы немесе болмауы;
- электр элементтің вольт амперлік сипаттамасының сипатына байланысты;
- электр тізбегіне енгізу мөлшеріне байланысты.
Пассивті тізбек деп электр энергия көзінен тұрмайтын тізбекті айтады. Мұндай тізбекте тек активті және реактивті элементтер болады.
Активті тізбек деп ең болмағанда бір электр энергия көзінен тұратын тізбекті айтады. Активті тізбекке күшейткіш элементтері бар тізбектер де жатады - транзисторлар және электронды шамдар, себебі олардың алмастыру сызбасына электр энергия көзі кіреді.
Барлық пассивті және активті тізбектер, өз кезегінде, реактивті және активті деп бөлінеді.
Реактивті тізбек деп тек реактивті элементтерден тұратын тізбек. Мұндай тізбектерде активті элементтер жоқ, ал реактивті элементтерді идеалды деп есептейді.
Сызықты электр тізбегі тек сызықты вольтамперлік сипаттамасы бар тізбек. Сызыкты емес электр тізбегі ең болмаганда бір сызықты емес вольтамперлік сипаттамасы бар тізбек.
ЭЛЕКТР ЭЛЕМЕНТТЕРІН ЖАЛҒАУ ТҮРЛЕРІ
Тізбектей жалғау- БІРДЕЙ ТОҚ өтетін элементтердің қосылу түрі. 3 суретге тек екі резистор тізбектей қосылған, ол Rз және R4 резисторлары.
Сурет 3 - Элементтерді типтік қосу түрлерінің сызбасы
Параллель жалғау - бірдей кернеу берілетін элементтердің қосылу түрі. 3 суретте екі резистор параллельді қосылған, ол R8 және R9 резисторлары.
Жұлдызша жалғау - түйіннен үш немесе одан да көп элементтері бар тармақтар шығатын жалғау түрі. Жұлдызша үш немесе одан да көп элементтері бар сәулелерден тұра алады. 3 суретте жұлдызша жалғауды мысалы, мына элементтер құрады: R 5 –R 6 –R 7, R 1 –R 2 –R 5 жэне т.б.
Үшбұрыш жалғау - үш тармақтар тұйық контур түзетін жалғану түрі. Мысалы, 3 суреттегі сызбада үшбұрышты жалғанган резисторлар R6–R7–R8, R2-R5-R7.
Эквивалентті түрлендіру тізбектегі екі немесе одан да көп элементтерді осындай элементтермен ауыстыруды білдіреді, мұнда қалған элементтердің электр режимдері өзгермейді, яғни, бұл элементтердегі тоқтар мен кернеулер бұрынғыдай қалады.
Кедергілер тізбектей қосылған кезде осы резистордың кедергілерінің қосындысына тең резистормен ауыстыруға болады. Осылайша, 4 суретте берілген сызбада мынаған ие боламыз:
Сурет 4 - элементтерді тізбектей (а) және парелелль (б) косқандағы
эквивалентті түрлендірулер
Егер тізбектей п түрлі резисторлар қосылса, онда олардың эквивалентті кедергісі мынаған тең:
Жеке жағдайда, егер п тізбектей қосылған резисторлар бірдей мәнді кедергіге R ие болса, онда олардың эквивалентті кедергісі п есе осы кедергінің, шамасынан үлкен болады:
R экв = nR.
Көрініп тұргандай, эквивалентті кедергінің шамасы тізбектей қосылған резисторлардан үлкенірек болады.
Параллель жалғанған резисторлар әрбір резистордың өткізгіштігінің қосындысына тең бір резистормен алмастыруға болады.
Резистор өткізгіштігі резистордың кедергісіне кері шама болып табылады және G белгіленеді:
4 суретте келтірілген сызба үшін: 
.
Кедергілер арқылы өткізгіштікті өрнектейміз:
.
R экв қатысты өрнекті анықтай отырып, мынаны анықтаймыз:
.
п параллель жалғанған кедергілер мынаған тең:
; 
.
Параллель жалғанған резисторлардың ерекшеліктерін айта кетейік. Көрініп тұрғандай, параллель жалғанған резисторлардың эквивалентті өткізгіштігі барлық резисторлар арасында ең көп мәнге ие резистордың өткізгіштігінен үлкен. Бұл резистор барлық резисторлар арасында ең аз кедергіге тең. Сондықтан, параллель жалғанған резисторлардың эквивалентті кедергісі барлық резисторлар арасында ең аз кедергіге ие. Бұдан, қандай да бір тізбекке резисторды паралелль жалғағанда бүл тізбектің жалпы (эквивалентті) кедергісін азайтады.
Егер бірдей кедергісі R бар п резисторлар паралелль жалғанса, олардың эквивалента кедергісі:
; 
Яғни, мұндай тізбектің эквивалента кедергісі барлық кедергіден п есе аз болады.
Жұлдызша және үшбұрыш жалғау. Жеке сызбаларды эквивалентті түрлендіріп, кіріс енгізулеріне қатысты олардың толық кедергісін табуға болмайды, егер жұлдызша электр элементінен үшбұрышқа немесе керісінше ауыстырмаса.
Сурет 5 - элементтердің жұлдызша (а) және үшбұрыш (б) бойынша электрлік жалғануы
Жұлдызшаны (сурет 5, а) эквивалентті үшбұрышқа (сурет 5, б) ауыстырғанда үшбұрыш кедергілері жұлдызшаның кедергілерімен келесідей қатынастар арқылы байланысады:
Үшбұрышты эквивалентті жұлдызшаға ауыстырғанда жұлдызшаның кедергілері үшбұрыш кедергілерімен келесідей қатынастар арқылы байланысады:
, 
, 
.
6 суретте а - б нүктесіне қатысты барлық тізбектің эквивалентті кедергілерін анықтау үшін эквивалента кедергінің тізбектелген тізбегі көрсетілген. Әдетте, түрлендіру тізбектей немесе паралелль косылған элементгерден басталады. Берілген сызбада (сурет 6, а) мұндай қосылыстар жоқ. Бұл жағдайда жұлдызшаны үшбұрышқа немесе үшбұрышты жұлдызшаға түрлендіруді орындау керек. Берілген сызбада R 2– R 5– R 3 резисторлы жұлдызшаны R 1,3, R 2,5, R 3,2 резисторлы үшбұрышпен (сурет 6, б) ауыстырайық, олардың шамасы жоғарыда келтірілген формулалардан табылады. Енді көрінгендей, R 4 және R 2,5 резисторлары және де R 6 және R 3,2 резисторлар өзара паралелль жалғанған және сәйкесінше R '4, R '6 резисторларымен (сурет 6, в) біріктіріледі. Кейін тізбектей жалғанған R '4 және R '6 резисторлар параллель жалғанған R 1,3 резистормен жалғанады. Олардың эквиваленті R '2 резисторы (сурет 9, г) болып табылады. R 1 және R '2, қоса отырып, барлық тізбек үшін R экв анықтаймыз (сурет 6, д)
Сурет 6 – Электр тізбегін эквивалентті түрлендіру реті
СЫЗЫҚТЫҚ ЭЛЕКТР ТІЗБЕКТЕРІН ЕСЕПТЕУ ӘДІСТЕРІ
ЭКВИВАЛЕНТТІ ТҮРЛЕНДІРУ ӘДІСІ
Бұл әдіс өте күрделі емес пассивті электр элементтері үшін қолданылады, мұндай тізбектер өте жиі кездеседі, сондықтан ол кеңінен таралған. Әдістің негізгі мағынасы бойынша электрлік тізбегін тізбекті түрде 7 суретте көрсетілген бір эквивалентті элементке дейін түрленеді («жиналады») және кіріс тоғы анықталады. Кейін бастапқы сызбаға («ашылады») біртіндеп тоқтар мен кернеулерді тізбектей анықтау арқылы жүзеге асырылады.
Есептеу реті:
1. Тоқтар мен кернеулердің шартты - оң бағыттары белгіленеді.
2. Кезең кезеңімен тізбектің участоктары түрлендіріледі. Және де әр кезенде түрлендіруден кейін жаңадан алынган сызба бойынша тоқтар мен кернеулер 1 ереже бойынша койылады.
3. Эквивалентті түрлендіру нәтижесінде тізбектің эквивалентті кедергінің шамасы анықталады.
4. Ом заңының көмегімен тізбектің кіріс тоғы аныкталады
5. Кезең кезеңімен қайта отырып, тізбектей, барлық тоқтар мен кернеулер анықталады.
Бұл әдісті мысалын 7 суретте келтірейік. Берілген сызбада тармақтардағы тоқтардың және элементтердегі кернеулердің шартты - оң бағыттарын қоямыз. Берілген полярлығы бар Е көзі әсерінен тоқтар мен кернеулердің бағыты тілшелермен берілген. Әдісті ары қарай түсіну үшін қолайлы болу үшін а және б түйіндерін белгілейік. Қарапайым есептеу кезінде мұны жасауға болмайды.
Ары қарай сызбаның тізбектей эквивалентті түрлендірілуі жүзеге асырылады. Ең алдымен паралелль жалғанған элементтерді біріктіріп анықтаймыз (сурет 7, 6):
Сурет 7 - тізбекті эквивалентті түрлендіру әдісімен есептеу мысалы
Кейін, барлық тізбектей жалғанған элементтерді біріктіре отырып, сызбаның эквивалентті түрлендіруін аяқтаймыз (сурет 10, в):
Соңғы сызбадан (сурет 7, в) I 1 тоқты табамыз:
Енді алдыңгы сызбаға қайтып ораламыз (сурет 7, б). Біз көріп отырғандай
табылған I 1 тоғы R 1, R 2,3, R 4 арқылы өтеді және онда кернеудің түсуін туғызады. Осы кернеулерді анықтаймыз:
.
Бастапқы сызбаға орала отырып (сурет 7, а), көрініп тұрғандай, табылған U аб кернеу R2 және R 3 элементтерге түсіріледі.
Яғни, былай жазуға болады U 2 = U 3 = U а,б
Бұл элементтердегі тоқтарды көрініп тұрган қатынастардан табады:
Сонымен, сызба анықталды.
Не нашли, что искали? Воспользуйтесь поиском: