
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры генетической оптимизации
В этом разделе мы подробно объясним как в действительности работает генетический алгоритм на двух простых примерах.
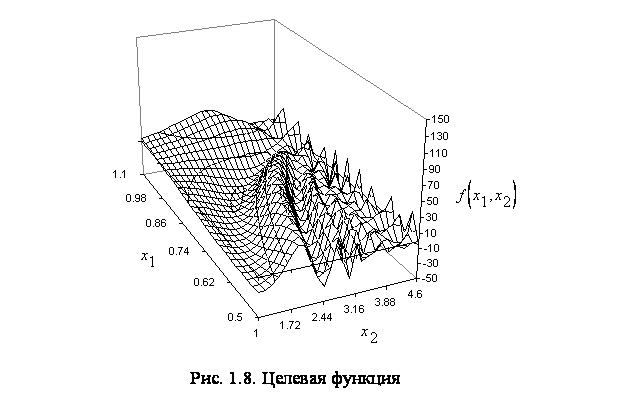
Пример 1.9. Задача оптимизации. Рассмотрим нелинейную целевую функцию с ограничениями:

0.5 

 1.1, 1.0
1.1, 1.0 

 4.6
4.6
Требуется найти: 
Поверхность целевой функции показана на рис. 1.8.
Кодирование. Для реализации генетического алгоритма необходимо закодировать оптимизируемые параметры в двоичные строчки. Длина строчки зависит от требуемой точности. Например, пусть переменная  имеет интервал изменения
имеет интервал изменения  , и требуемая точность - пять знаков после запятой. В этом случае интервал изменения переменной
, и требуемая точность - пять знаков после запятой. В этом случае интервал изменения переменной  должен быть разбит как минимум на
должен быть разбит как минимум на  квантов. Требуемое число битов
квантов. Требуемое число битов  находится по формуле:
находится по формуле:

Обратное преобразование строки битов в действительное значение переменной  выполняется по следующей формуле:
выполняется по следующей формуле:
 десятичное_число (строка_битов
десятичное_число (строка_битов  )
)  ,
,
где десятичное_число (строка_битов  ) представляет собой десятичное значение, закодированное в бинарной строке строка_битов
) представляет собой десятичное значение, закодированное в бинарной строке строка_битов 
Предположим, что требуемая точность составляет 5 знаков после запятой. Найдем число битов, необходимых для кодирования переменных  и
и  :
:
(1.1 - 0.5)  100,000 = 60,000
100,000 = 60,000
2 
 60,000
60,000  2
2  - 1,
- 1, 
(4.6 - 1.0)  100,000 = 360,000
100,000 = 360,000
2 
 360,000
360,000  2
2  - 1,
- 1, 
 .
.
Суммарная длина хромосомы составляет 35 битов, которые можно представить следующим образом:

Соответствующие значения переменных  и
и  даны ниже:
даны ниже:
| Двоичное число | Десятичное число | |

| ||

|
 = 0.5 + 16722
= 0.5 + 16722 
 0.65310,
0.65310,
 = 1.0 + 319230
= 1.0 + 319230 
 3.19198.
3.19198.
Исходная популяция. Исходная популяция генерируется случайно:
v  = =
| [01000001010100101001101111011111110] |
v  = =
| [10001110101110011000000010101001000] |
v  = =
| [11111000111000001000010101001000110] |
v  = =
| [01100110110100101101000000010111001] |
v  = =
| [00000010111101100010001110001101000] |
v  = =
| [10111110101011011000000010110011001] |
v  = =
| [00110100010011111000100110011101101] |
v  = =
| [11001011010100001100010110011001100] |
v  = =
| [01111110001011101100011101000111101] |
v 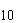 = =
| [01111101001110101010000010101101010] |
Соответствующие значения переменных  и
и  имеют вид:
имеют вид:
v  = [ = [  ] = ] =
| [0.653097, 3.191983] |
v  = [ = [  ] = ] =
| [0.834511,2.809287] |
v  =[ =[  ] = ] =
| [1.083310,2.874312] |
v  =[ =[  ] = ] =
| [0.740989,3.926276] |
v  =[ =[  ]= ]=
| [0.506940,1.499934] |
v  =[ =[  ]= ]=
| [0.946903,2.809843] |
v  =[ =[  ]= ]=
| [0.622600,2.935225] |
v  =[ =[  ]= ]=
| [0.976521,3.778750] |
v  =[ =[  ]= ]=
| [0.795738,3.802377] |
v 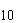 =[ =[  ] = ] =
| [0.793504,3.259521] |
Функция соответствия. Оценка функции соответствия хромосомы выполняется в три шага:
1°. Преобразовать генотип хромосомы в фенотип. В данной задаче это означает преобразование двоичной строчки в соответствующее действительное значение 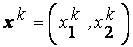 ,
,  , где
, где  - число вариантов в исходной популяции.
- число вариантов в исходной популяции.
2°. Вычислить целевую функцию  .
.
3°. Преобразовать целевую функцию в значение функции соответствия. Для решаемой задачи оптимизации функция соответствия эквивалентна целевой функции.  ,
,  .
.
Функция соответствия играет роль среды и оценивает хромосомы по степени их приспособленности к выполнению критерия оптимизации.
Значения функций соответствия вышеприведенных хромосом следующие:
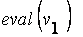 = =
| f (0.653097,3.191983) = 20.432394 |
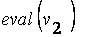 = =
| f (0.834511,2.809287) = -4.133627 |
 = =
| f (1.083310,2.874312) = 28.978472 |
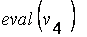 = =
| f (0.740989,3.926276) = -2.415740 |
 = =
| f (0.506940,1.499934) = -2.496340 |
 = =
| f (0.946903,2.809843) = -23.503709 |
 = =
| f (0.622600,2.935225) = -13.878172 |
 = =
| f (0.976521,3.778750) = -8.996062 |
 = =
| f (0.795738,3.802377) = 6.982708 |
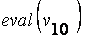 = =
| f (0.793504,3.259521) = 6.201905 |
Очевидно, что хромосома  наиболее сильная, а хромосома
наиболее сильная, а хромосома  наиболее слабая.
наиболее слабая.
Отбор. Наибольшее распространение на практике получил подход, называемый колесо рулетки [58] (от англ. roulette wheel). Согласно этому подходу отбор осуществляется на основе некоторой функции распределения, которая строится пропорционально вычисленным функциям соответствия сгенерированных вариантов-хромосом. Колесо рулетки может быть сконструировано следующим образом:
1. Вычисляем значение функции соответствия  для каждой хромосомы
для каждой хромосомы  :
:
 ,
,  .
.
2. Вычисляем общую функцию соответствия популяции:

3. Вычисляем вероятность отбора  для каждой хромосомы
для каждой хромосомы  :
:
 ,
,  .
.
4. Вычисляем совокупную вероятность  для каждой хромосомы
для каждой хромосомы  :
:
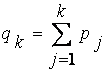 ,
,  .
.
Процесс отбора начинается с вращения колеса  раз; при этом каждый раз выбирается одна хромосома по следующему алгоритму:
раз; при этом каждый раз выбирается одна хромосома по следующему алгоритму:
1°. Генерируем случайное число  из интервала
из интервала  .
.
2°. Если  , то выбираем первую хромосому
, то выбираем первую хромосому  ; иначе выбираем
; иначе выбираем  -ую хромосому
-ую хромосому  (
( ) такую, что
) такую, что  .
.
Общая функция соответствия  всей популяции равна:
всей популяции равна:
 242.208919.
242.208919.
Вероятность отбора  для каждой хромосомы
для каждой хромосомы  (
( ) равна:
) равна:
 = 0.181398, = 0.181398,
|  = 0.079973, = 0.079973,
|  = 0.216681, = 0.216681,
|
 = 0.087065, = 0.087065,
| 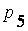 = 0.086732, = 0.086732,
|  = 0.000000, = 0.000000,
|
 = 0.039741, = 0.039741,
|  = 0.059897, = 0.059897,
|  = 0.125868, = 0.125868,
|
 = 0.122645. = 0.122645.
|
Совокупные вероятности  для каждой хромосомы
для каждой хромосомы  (
( ) равны:
) равны:
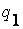 = 0.181398, = 0.181398,
|  = 0.261370, = 0.261370,
|  = 0.478052, = 0.478052,
|
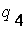 = 0.565117, = 0.565117,
|  = 0.651849, = 0.651849,
|  = 0.651849, = 0.651849,
|
 = 0.691590, = 0.691590,
|  = 0.751487, = 0.751487,
|  = 0.877355, = 0.877355,
|
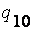 = 1.000000. = 1.000000.
|
Теперь мы готовы вращать колесо рулетки 10 раз и каждый раз отобрать одну хромосому для новой популяции. Допустим, что случайная последовательность 10 чисел из интервала  имеет вид:
имеет вид:
| 0.301431 | 0.322062 | 0.766503 | 0.881893 |
| 0.350871 | 0.583392 | 0.177618 | 0.343242 |
| 0.032685 | 0.197577. |
Первое число  0.301431 больше чем
0.301431 больше чем  и меньше чем
и меньше чем  . Это означает, что отбирается хромосома
. Это означает, что отбирается хромосома  . Второе число
. Второе число  0.322062 также больше чем
0.322062 также больше чем  и меньше чем
и меньше чем  . Значит опять отбираем хромосому
. Значит опять отбираем хромосому  для новой популяции; и т.д. Наконец, получим новую популяцию, состоящую из таких хромосом:
для новой популяции; и т.д. Наконец, получим новую популяцию, состоящую из таких хромосом:
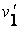 = =
| [11111000111000001000010101001000110] | 
|
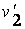 = =
| [11111000111000001000010101001000110] | 
|
 = =
| [11001011010100001100010110011001100] | 
|
 = =
| [01111110001011101100011101000111101] | 
|
 = =
| [11111000111000001000010101001000110] | 
|
 = =
| [01100110110100101101000000010111001] | 
|
 = =
| [01000001010100101001101111011111110] | 
|
 = =
| [11111000111000001000010101001000110] | 
|
 = =
| [01000001010100101001101111011111110] | 
|
 = =
| [10001110101110011000000010101001000] | 
|
Скрещивание. Для скрещивания хромосом будем использовать метод с одной точкой обмена. В соответствие с этим методом, случайно выбирается одна точка обмена, относительно которой меняются местами части хромосом-родителей. Для примера рассмотрим скрещивание двух хромосом, для которых была случайно выбрана точка обмена после 17-го гена:

В результате обмена частей родительских хромосом получаются следующие хромосомы-отпрыски:

Пусть вероятность скрещивания  , т. е. в среднем 25% хромосом подвергнуться скрещиванию. Таким образом, скрещивание осуществляется по такому алгоритму:
, т. е. в среднем 25% хромосом подвергнуться скрещиванию. Таким образом, скрещивание осуществляется по такому алгоритму:
Процедура: Скрещивание.
Begin
 :=0;
:=0;
while ( ) do
) do
 := случайное число из интервала [0,1];
:= случайное число из интервала [0,1];
if (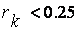 ) then
) then
отобрать хромосому  как одного из родителей для скрещивания;
как одного из родителей для скрещивания;
end;
 ;
;
end;
end.
Предположим, что сгенерирована последовательность случайных чисел:
| 0.625721 | 0.266823 | 0.288644 | 0.295114 |
| 0.163274 | 0.567461 | 0.085940 | 0.392865 |
| 0.770714 | 0.548656. |
Это означает, что хромосомы  и
и  выбираются для скрещивания. После этого мы генерируем случайное целое число
выбираются для скрещивания. После этого мы генерируем случайное целое число  (позиция) из промежутка [1,34] (так как общая длина хромосомы равна 35) и считаем его точкой обмена хромосом или, другими словами, точкой скрещивания. Предположим, что было сгенерировано число
(позиция) из промежутка [1,34] (так как общая длина хромосомы равна 35) и считаем его точкой обмена хромосом или, другими словами, точкой скрещивания. Предположим, что было сгенерировано число  равное 1, т. е. хромосомы-родители обмениваются частями после первого бита и появятся следующие хромосомы-отпрыски:
равное 1, т. е. хромосомы-родители обмениваются частями после первого бита и появятся следующие хромосомы-отпрыски:

Мутация. Мутация состоит в изменении одного или большего числа генов с вероятностью равной коэффициенту мутации. Допустим, что 18-й ген хромосомы 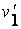 подвергается мутации. Так как мы имеем дело с бинарными строчками, то мутация заключается в инверсии соответствующего бита:
подвергается мутации. Так как мы имеем дело с бинарными строчками, то мутация заключается в инверсии соответствующего бита:

Зададим коэффициенту мутации значение  , так что в среднем 1% всех битов популяции подвергнуться операции мутации. Число битов во всей популяции составляет
, так что в среднем 1% всех битов популяции подвергнуться операции мутации. Число битов во всей популяции составляет  битов. Поэтому в среднем в каждом поколении мутирует 3.5 бита. Каждый бит имеет одинаковый шанс подвергнуться мутации. Таким образом, мы должны сгенерировать последовательность случайных чисел
битов. Поэтому в среднем в каждом поколении мутирует 3.5 бита. Каждый бит имеет одинаковый шанс подвергнуться мутации. Таким образом, мы должны сгенерировать последовательность случайных чисел 
 из интервала [0,1]. Предположим, что мутируют следующие гены:
из интервала [0,1]. Предположим, что мутируют следующие гены:
| Позиция бита в популяции | Номер хромосомы | Позиция бита в хромосоме | Случайное число 
|
| 0.009857 | |||
| 0.003113 | |||
| 0.000946 | |||
| 0.001282 |
После мутации получается следующая популяция:
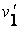 = =
| [11111000111000001000010101001000110] |
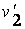 = =
| [11111000111000001000010101001000110] |
 = =
| [11001011010100001100010110011001100] |
 = =
| [01111010001011101100011101000111101] |
 = =
| [11000001010100101001101111011110110] |
 = =
| [01100110110100101101000000010111001] |
 = =
| [11111000111000001000010101001000110] |
 = =
| [11111000111000001000010101001000110] |
 = =
| [01000001010100101001101111011111110] |
 = =
| [10001110101110011000000010101000000]. |
Соответствующие десятичные значения переменных  и
и  и значения функции соответствия имеют вид:
и значения функции соответствия имеют вид:
f (1.083310,2.874312)=28.978472
f (1.083310,2.874312)=28.978472
f (0.976521,3.778750)=-8.996062
f (0.786363,3.802377)=9.366723
f (0.953101,3.191928)=-23.229745
f (0.740989,3.926276)=-2.415740
f (1.083310,2.874312)=28.978472
f (1.083310,2.874312)=28.978472
f (0.653097,3.191983)=20.432394
f (0.834511,2.809232)=-4.138564
Таким образом, завершена одна итерация генетического алгоритма. Проделав 1000 итераций, мы получим наилучшую хромосому в 419-м поколении:
 = [01000011000100110110010011011101001]
= [01000011000100110110010011011101001]
 = f (0.657208,2.418399) = 31.313555
= f (0.657208,2.418399) = 31.313555
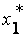 = 0.657208
= 0.657208  = 2.418399
= 2.418399
 = 31.313555.
= 31.313555.
Пример 1.10. Синтез текста. Этот пример прекрасно демонстрирует мощь генетических алгоритмов. Задача синтеза текста заключается в получении фрагмента известной украинской песни несе Галя воду
из случайно сгенерированного списка букв при помощи генетического алгоритма. Так как для каждой позиции текста возможны 32 различные буквы алфавита, а таких позиций в заданном выражении 12, то вероятность получения необходимой строки случайным способом равна  , т. е. практически нуль.
, т. е. практически нуль.
Для кодирования строки букв будем использовать кодовую таблицу символов ASCII (в операционной системе Windows). Тогда строка несе Галя воду преобразуется в следующую хромосому:
[237, 229, 241, 229, 227, 224, 235, 255, 226, 238, 228, 243]
Сгенерируем исходную популяцию из 10 случайных фраз:
[232, 239, 225, 242, 227, 238, 255, 227, 186, 238, 236, 239]
[228, 226, 244, 231, 231, 224, 226, 224, 237, 248, 243, 247]
[252, 241, 243, 228, 228, 225, 246, 225, 234, 186, 230, 246]
[249, 227, 252, 249, 244, 245, 236, 229, 248, 252, 224, 226]
[230, 232, 234, 245, 231, 254, 227, 245, 238, 247, 242, 232]
[232, 228, 227, 245, 230, 226, 232, 179, 247, 255, 238, 186]
[232, 248, 231, 235, 248, 179, 235, 186, 224, 255, 252, 242]
[239, 248, 236, 229, 179, 233, 232, 244, 249, 245, 252, 230]
[249, 232, 236, 229, 240, 244, 227, 243, 230, 244, 254, 242]
[248, 230, 231, 252, 245, 239, 242, 254, 252, 255, 240, 255]
Теперь преобразуем эти хромосомы в строки символов и увидим, что получится 10 бессмысленных фраз:
ипбтгоягєомп
двфззаваншуч
ьсуддбцбкєжц
щгьщфхмешьав
жикхзюгхочти
идгхжви_чяоє
ишзлш_лєаяьт
пшме_йифщхьж
щимерфгужфют
шжзьхптюьяря.
Функция соответствия вычисляется как число правильно отгаданных букв. Например, функция соответствия для строки <ипбт г оягє о мп> равна 2. В табл. 1.2 приведен список хромосом, которые были наилучшими на каждой из 32-х итераций генетического алгоритма.
Таблица 1.2
Лучшие хромосомы на каждой итерации
| Поко-ление | Строка | Функция соответствия | Поколение | Строка | Функция соответствия |
| ипбтгоягєомп | несечалядгду | ||||
| ипбтгоягєомп | несечалядгду | ||||
| ипбтгоягєомп | несегалядгду | ||||
| никхгаваншйт | несегалядгду | ||||
| ндмералядгжц | несегалядгду | ||||
| ндмералядгжц | несегалядгду | ||||
| ндмералядгжц | несегалядгду | ||||
| ндшеьалявгжц | несегалядоду | ||||
| ндшеьалявгжц | несегалядоду | ||||
| ндшеьалявгжц | несегалядоду | ||||
| нисералядгжу | несегалядоду | ||||
| нисералядгжу | несегалядоду | ||||
| нисералядгжу | несегалядоду | ||||
| несеролядгду | несегалядоду | ||||
| несеролядгду | несегалядоду | ||||
| несеролядгду | несегаляводу |
Нейронные сети
Этот раздел написан по материалам работ [8,12,60]. С дополнительными сведениями по нейронным сетям можно познакомиться в работах [1,4,19,65, 76,78,79,82].
Основные понятия
Проблема машинной имитации человеческих мыслей воодушевляет ученых уже несколько столетий. Более 50 лет назад были созданы первые электронные модели нервных клеток. Кроме того, появлялись много работ по новым математическим моделям и обучающим алгоритмам. Сегодня так называемые нейронные сети представляют наибольший интерес в этой области. Они используют множество простых вычислительных элементов, называемых нейронами, каждый из которых имитирует поведение отдельной клетки человеческого мозга. Принято считать, что человеческий мозг - это естественная нейронная сеть, а модель мозга - это просто нейронная сеть. На рис. 1.9 показана базовая структура такой нейронной сети.

Рис. 1.9. Базовая структура нейронной сети
Каждый нейрон в нейронной сети осуществляет преобразование входных сигналов в выходной сигнал и связан с другими нейронами. Входные нейроны формируют так называемый интерфейс нейронной сети. Нейронная сеть, показанная на рис. 1.9, имеет слой, принимающий входные сигналы, и слой, генерирующий выходные сигналы. Информация вводится в нейронную сеть через входной слой. Все слои нейронной сети обрабатывают эти сигналы до тех пор, пока они не достигнут выходного слоя.
Задача нейронной сети - преобразование информации требуемым образом. Для этого сеть предварительно обучается. При обучении используются идеальные (эталонные) значения пар <входы-выходы> или <учитель>, который оценивает поведение нейронной сети. Для обучения используется так называемый обучающий алгоритм. Ненастроенная нейронная сеть не способна отображать желаемого поведения. Обучающий алгоритм модифицирует отдельные нейроны сети и веса ее связей таким образом, чтобы поведение сети соответствовало желаемому поведению.
Не нашли, что искали? Воспользуйтесь поиском: