
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Нечеткость и вероятность
Новички в теории нечетких множеств часто пытаются сопоставить ее с теорией вероятности. Однако, обе эти теории трудно сравнивать поскольку они по-разному формализуют неопределенность. В теории вероятностей рассматривается статистическая неопределенность, например, вероятность поражения цели равна 0.9. Теория нечетких множеств позволяет работать с лингвистической неопределенностью, например, меткий стрелок. Эти виды неопределенности формализуются с помощью:
· функций распределения - в теории вероятностей,
· функций принадлежности - в теории нечетких множеств.
Принципиальное различие двух указанных распределений иллюстрирует пример, который любит приводить основоположник теории нечетких множеств Л. Заде [85].
Пример 1.8. Рассмотрим утверждение <Автор съедает  яиц на завтрак>,
яиц на завтрак>,
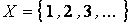 .
.
Величине  , которая является неопределенным параметром, могут соответствовать распределения возможности и вероятности.
, которая является неопределенным параметром, могут соответствовать распределения возможности и вероятности.
Распределение возможности  может быть интерпретировано как степень (субъективная мера) легкости, с которой Автор съедает
может быть интерпретировано как степень (субъективная мера) легкости, с которой Автор съедает 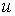 яиц. Для определения вероятностного распределения
яиц. Для определения вероятностного распределения  необходимо проследить за Автором на протяжение 100 дней.
необходимо проследить за Автором на протяжение 100 дней.
Оба распределения представлены ниже.
Распределение возможности и вероятности
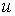
| ||||||||
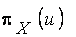
| 0.8 | 0.6 | 0.4 | 0.2 | ||||

| 0.1 | 0.8 | 0.1 |
Мы видим, что высокая степень возможности  никак не означает такую же высокую степень вероятности
никак не означает такую же высокую степень вероятности  . Но бесспорно одно: если событие невозможно, то оно также и невероятно.
. Но бесспорно одно: если событие невозможно, то оно также и невероятно.
Принципиальное отличие теории вероятности от теории возможности состоит в том, что в этих теориях по-разному выполняется аксиома дополнения:
 - для теории вероятности.
- для теории вероятности.
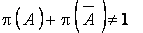 - для теории возможности.
- для теории возможности.
Не нашли, что искали? Воспользуйтесь поиском: