ВВЕДЕНИЕ В ИНТЕЛЛЕКТУАЛЬНЫЕ ТЕХНОЛОГИИ

Нечеткие множества

Этот раздел написан по материалам работ [15,18,25]. С дополнительными сведениями по нечетким множествам можно познакомиться по работам [26,57,64,80,83-85].

Теория множеств представляет собой мощный инструмент математики. Однако, лежащая в ее основе аксиома исключенного третьего, утверждающая, что элемент либо принадлежит множеству либо не принадлежит, часто делает эту теорию неприменимой в реальных задачах, в которых применяются нечеткие оценки, такие как: <большая прибыль>, <высокое давление>, <умеренная температура>, <надежные инструменты>, <безопасные условия> и т.п. К сожалению, подобные высказывания не могут быть адекватно формализованы обычными математическими методами.

Если мы хотим учесть точное значение нечеткого терма, то четкое разделение элементов (например значений давления) на те, которые принадлежат терму <высокое>, и те, которые не принадлежат, является искусственным. Это происходит в первую очередь потому, что некоторые значения могут восприниматься как <высокое давление с некоторой натяжкой>, <не совсем высокое давление>, <не совсем невысокое давление> и др.

Попытка развития формального аппарата для вовлечения частичной принадлежности в теорию множеств была предпринята в середине 60-х годов Заде [15]. Он ввел понятие нечеткого множества как собрания элементов, которые могут принадлежать этому множеству со степенью от 0 до 1. Причем 0 обозначает абсолютную непринадлежность, а 1 - абсолютную принадлежность множеству. Это было сделано путем применения понятия функции принадлежности, которая ставит в соответствие каждому элементу универсального множества число из интервала [0,1], обозначающее степень принадлежности. Понятие функции принадлежности является обобщением понятия характеристической функции четкого множества, которая оперирует значениями 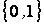. Поэтому основные свойства и операции над нечеткими множествами, введенные Заде и его многочисленными последователями, являются обобщениями соответствующих свойств и операций классической теории множеств.

С момента своего возникновения теория нечетких множеств вызвала беспрецедентный рост интереса практически во всех отраслях науки и техники.

Основные понятия теории нечетких множеств

Пусть - универсальное множество, т.е. полное множество, охватывающее всю проблемную область.

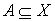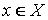Определение 1.1. Нечеткое множество представляет собой набор пар , где и - функция принадлежности, которая представляет собой некоторую субъективную меру соответствия элемента нечеткому множеству .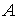

может принимать значения от нуля, который обозначает абсолютную не принадлежность, до единицы, которая, наоборот, говорит об абсолютной принадлежности элемента нечеткому множеству 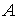. Иногда удобно рассматривать значение как степень совместимости элемента с размытым понятием, представленным нечетким множеством .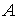

Часто нечеткое множество 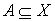и его функцию принадлежности рассматривают как взаимозаменяемые понятия.

Если множество заменить на 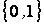, то функция принадлежности будет представлять собой характеристическую функцию обыкновенного (не нечеткого) множества.

Если нечеткое множество 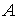определено на конечном универсальном множестве , то его удобно обозначать следующим образом:

,

где < > - пара <функция принадлежности / элемент>, называемая синглтоном, а < + > - обозначает совокупность пар.

Пример 1.1. Пусть . Тогда нечеткое множество <большие числа> может быть представлено следующим образом:

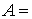<большие числа>=0.2/6 + 0.5/7 + 0.8/8 + 1/9 + 1/10.

Это можно понимать следующим образом: 9 и 10 с абсолютной уверенностью можно отнести к <большим числам>, 8 есть <большое число> со степенью 0.8 и т.д. 1,2,...5 абсолютно не являются <большими числами>.

На практике удобно использовать кусочно-линейную аппроксимацию функции принадлежности нечеткого множества как это показано на рис. 1.1, так как требуется только два значения - и .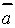

В случае непрерывного множества используется следующее обозначение:

.

(Знак в этих формулах обозначают совокупность пар).

Не нашли, что искали? Воспользуйтесь поиском: