Объект с дискретным выходом

Соотношения (5.3) позволяют вычислить вектор функций принадлежности выходной переменной 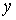к различным классам решений :

(5.7)

где , , и - векторы, введенные раннее.

Определим желаемый вектор функций принадлежности следующим образом:

(5.8)

Пусть обучающая выборка задана в виде пар экспериментальных данных:

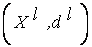, (5.9)

где и - входной вектор и соответствующий класс решений выходной переменной для 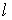-ой пары <вход-выход>, .

Для нахождения вектора неизвестных параметров , который минимизирует разницу между теорией (5.7) и экспериментом (5.9), воспользуемся методом наименьших квадратов. Задача оптимальной настройки нечеткой модели формулируется следующим образом:

найти вектор , который удовлетворяет ограничениям

, , , , ,

и обеспечивает минимальное расстояние между желаемым и модельным векторами функций принадлежности

(5.10)

где

Для решения задач (5.6) и (5.10) в этой главе будут предложены генетические алгоритмы оптимизации.

Не нашли, что искали? Воспользуйтесь поиском: