Модифицированный принцип обобщения

Допущение 4.3. Будем предполагать, что функция

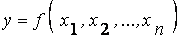
удовлетворяет следующим ограничениям:

Область изменения любого аргумента непрерывна.

На области определения функция дифференцируема.

Множество аргументов можно представить объединением не более, чем трех подмножеств причем:

;

;

;

.

Обратим внимание, что - знакопеременная функция и для всех 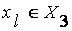, знак производной не зависит от т.е.:

.

Перечисленные ограничения введены на основе анализа аналитических моделей, которые используются в практических расчетах.

Определение 4.8. Модифицированный принцип обобщения.

Пусть 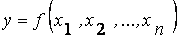- функция от 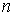переменных, удовлетворяющая допущениям 4.3. Аргументы функции 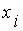- суть нечеткие числа в виде

, .

Нечетким обобщением назовем число:

,

где

Эквивалентность результатов применения модифицированного и известных принципов обобщения доказывается в следующем предложении.

Предложение 4.7. Если нечеткие числа представлены в виде разложения по -уровневым множествам и функция подчиняется допущениям 4.3, то результаты нечеткого обобщения по определениям 4.6 и 4.8 совпадают.

Доказательство. Если нечеткие числа задаются в виде -уровневого разложения, то принцип обобщения Заде эквивалентен определению 4.7. Поэтому достаточно показать, что при допущениях 4.3 результаты применения определений 4.7 и 4.8 совпадают.

В предложении 4.6 доказано, что для любого -уровня

;

,

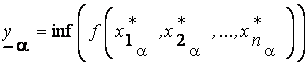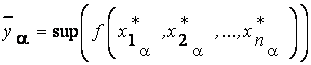где , .

Теперь необходимо найти максимальное и минимальное значение функции для каждого -уровня с учетом допущений 4.3.

Максимальное значение функции достигается при таких значениях аргументов:

, ,

Это обусловлено тем, что любое приращение аргументов в пределах заданной области не увеличивает значение функции.

Минимальное значение функции достигается при таких значениях аргументов:

, ,

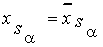Это обусловлено тем, что любое приращение аргументов в пределах заданной области не уменьшает значение функции.

Учитывая это, получаем следующую нечеткую модель:

,

где

Совпадение полученных результатов с определением 4.8, свидетельствует о справедливости предложения 4.7. Целесообразность использования модифицированного принципа обобщения вытекает из следующего предложения.

Предложение 4.8. Модифицированный принцип обобщения обладает меньшей вычислительной трудоемкостью по сравнению с классическим принципом обобщения Заде.

Доказательство. Пусть 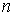- количество аргументов функций, а 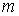-количество -уровней, на которых задан каждый аргумент. Рассмотрим трудоемкость применения каждого принципа.

Принцип обобщения Заде. Поскольку нечеткое число задается в точках, то, в соответствии с предложением 4.5, для применения принципа обобщения Заде необходимо перебрать вариантов.

Модифицированный принцип обобщения. В этом случае максимальное и минимальное значение функции находится аналитически для каждого из 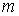-уровней. Поэтому число вариантов 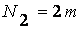. Отсюда следует существенно меньшая вычислительная трудоемкость (табл. 4.2).

Таблица 4.2.

Трудоемкость применения различных принципов обобщения

Принцип обобщения	Количество вариантов перебора
По Заде				4 096
Модифицированный

Не нашли, что искали? Воспользуйтесь поиском: