
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Обобщенное дерево логического вывода
Иерархическую взаимосвязь между входными переменными, классами входных переменных и выходной переменной (интегральным показателем) представим в виде дерева (рис. 3.5), которому соответствует система соотношений:
 (3.29)
(3.29)
 (3.30)
(3.30)
 (3.31)
(3.31)
 (3.32)
(3.32)
где  - выходная переменная (интегральный показатель);
- выходная переменная (интегральный показатель);
 -классы входных переменных;
-классы входных переменных;
 - входные переменные, отнесенные к классам
- входные переменные, отнесенные к классам  , причем
, причем  ,
,  ,
,  .
.
Дерево на рис. 3.5 отражает лишь двухуровневую иерархию входных переменных. Однако детализация может быть продолжена по уровням: класс - подкласс -группа-подгруппа и т.д.
Будем считать, что все переменные, стоящие в вершинах дерева (рис. 3.5), являются лингвистическими переменными со следующими термами:
 - множество термов для оценки переменной
- множество термов для оценки переменной  ;
;
 - множество термов для оценки переменной
- множество термов для оценки переменной  ;
;
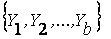 - множество термов для оценки переменной
- множество термов для оценки переменной  ;
;
 - множество термов для оценки переменной
- множество термов для оценки переменной  ;
;
 - множество термов для оценки переменной
- множество термов для оценки переменной 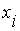 ,
,  ;
;
 - множество термов для оценки переменной
- множество термов для оценки переменной  ,
,  ;
;
 - множество термов для оценки переменной
- множество термов для оценки переменной  ,
,  .
.
Введенные множества термов обозначены на соответствующих ветвях дерева. Внутри каждого из множеств нечеткие термы упорядочены по принципу: от низшего к высшему, например { низкий, средний, высокий и т.д. }. Мощности всех множеств, т.е. числа термов, которые используются для оценки лингвистических переменных, входящих в соотношения (3.29)-(3.32), в общем случае могут быть различными.

Пользуясь понятиями универсального множества и функции принадлежности, каждый из термов представим в виде нечеткого множества:
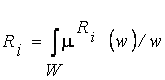 ,
,  ,
,  , (3.33)
, (3.33)
 ,
,  ,
,  , (3.34)
, (3.34)
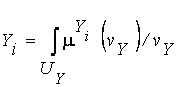 ,
,  ,
,  , (3.35)
, (3.35)
 ,
,  ,
,  , (3.36)
, (3.36)
 ,
,  ,
,  ,
,  , (3.37)
, (3.37)
 ,
,  ,
,  ,
,  , (3.38)
, (3.38)
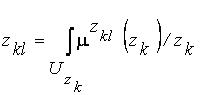 ,
,  ,
,  ,
,  , (3.39)
, (3.39)
где  - универсальное множество, на котором задана переменная
- универсальное множество, на котором задана переменная  , т.е.
, т.е.  ,
,  ;
;
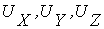 - универсальные множества, на которых заданы переменные
- универсальные множества, на которых заданы переменные 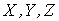 , т.е.
, т.е.  ,
,  ,
,  ;
;  - универсальные множества, на которых заданы переменные
- универсальные множества, на которых заданы переменные  ,
,  ,
,  ,
,  ;
;  - функция принадлежности переменной
- функция принадлежности переменной 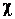 нечеткому терму
нечеткому терму  .
.
Информацию о соотношениях (3.29)-(3.32) будем представлять в виде нечетких баз знаний, содержащих логические высказывания о взаимосвязи входных и выходных переменных [34]. Нечеткая база знаний о соотношении (3.29) будет иметь следующий вид:
ЕСЛИ  И
И  И... И
И... И  ИЛИ
ИЛИ
 И
И  И... И
И... И  ИЛИ...
ИЛИ...
 И
И 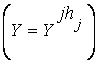 И... И
И... И  ,
,
ТО 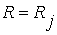 ,
,  . (3.40)
. (3.40)
Эти правила можно представить в виде матрицы знаний  :
:

| 
| ... 
| 
| |
 ...
...

|  ...
...

|  ...
...

| 
| |

| 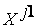 ...
...
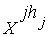
|  ...
...

|  ...
...

| ...
 ...
...
|
 ...
...

| 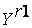 ...
...

|  ...
...

|

|
(3.41)
С применением операций пересечения 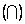 и объединения
и объединения  множеств перепишем нечеткую базу знаний (3.40) в следующей форме:
множеств перепишем нечеткую базу знаний (3.40) в следующей форме:
 ,
,  . (3.42)
. (3.42)
Нечеткая база знаний о соотношении (3.30) будет иметь следующий вид:
ЕСЛИ  И
И  И... И
И... И  ИЛИ
ИЛИ
 И
И  И... И
И... И  ИЛИ...
ИЛИ...
 И
И  И... И
И... И  ,
,
ТО 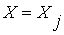 ,
,  . (3.43)
. (3.43)
Эти правила можно представить в виде матрицы знаний  :
:

| 
| ... 
| 
| |
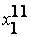 ...
...
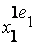
|  ...
...

|  ...
...

| 
| |

|  ...
...

|  ...
...

| 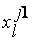 ...
...

| ...
 ...
...
|
 ...
...

| 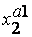 ...
...

|  ...
...

|

|
(3.44)
С применением операций пересечения 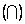 и объединения
и объединения  множеств перепи-шем нечеткую базу знаний (3.43) в следующей форме:
множеств перепи-шем нечеткую базу знаний (3.43) в следующей форме:
 ,
,  . (3.45)
. (3.45)
Нечеткая база знаний о соотношении (3.31) будет иметь следующий вид:
ЕСЛИ  И
И 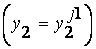 И... И
И... И  ИЛИ
ИЛИ
 И
И  И... И
И... И  ИЛИ...
ИЛИ...
 И
И  И... И
И... И 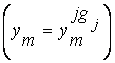 ,
,
ТО 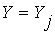 ,
,  . (3.46)
. (3.46)
Эти правила можно представить в виде матрицы знаний  :
:

| 
| ... 
| 
| |
 ...
...

|  ...
...

|  ...
...
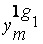
| 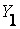
| |

| 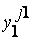 ...
...

| 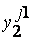 ...
...

|  ...
...

| ...
 ...
...
|
 ...
...

|  ...
...

|  ...
...

|

|
(3.47)
С применением операций пересечения 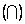 и объединения
и объединения  множеств перепишем нечеткую базу знаний (3.46) в следующей форме:
множеств перепишем нечеткую базу знаний (3.46) в следующей форме:
 ,
,  . (3.48)
. (3.48)
Нечеткая база знаний о соотношении (3.32) будет иметь следующий вид:
ЕСЛИ  И
И  И... И
И... И  ИЛИ
ИЛИ
 И
И  И... И
И... И  ИЛИ...
ИЛИ...
 И
И  И... И
И... И  ,
,
ТО 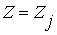 ,
,  . (3.49)
. (3.49)
Эти правила можно представить в виде матрицы знаний  :
:

| 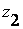
| ... 
| 
| |
 ...
...
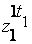
|  ...
...

|  ...
...

| 
| |
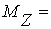
|  ...
...
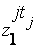
| 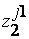 ...
...

| 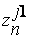 ...
...
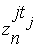
| ...
 ...
...
|
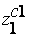 ...
...

|  ...
...
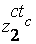
|  ...
...

|

|
С применением операций пересечения 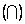 и объединения
и объединения  множеств перепишем нечеткую базу знаний (3.49) в следующей форме:
множеств перепишем нечеткую базу знаний (3.49) в следующей форме:
 ,
,  . (3.51)
. (3.51)
Таким образом, нами определена система нечетких логических высказываний (3.42), (3.45), (3.48), (3.51), которые описывают экспертную информацию о соотношениях (3.29)-(3.32), соответствующих обобщенному дереву взаимосвязи <входные переменные - выходная переменная>. Принципы кодирования лингвистических переменных и их нечетких термов, предложенные выше для двухуровневого дерева вывода, остаются неизменными для дерева произвольной размерности. Структура дерева, выбор термов лингвистических переменных на его ветвях, а также нечеткие базы знаний в каждой из нетерминальных вершин дерева, - все это определяет методику сбора экспертной информации, необходимой для построения модели нелинейного объекта.
Не нашли, что искали? Воспользуйтесь поиском: