
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Нечеткое представление неопределенных параметров
Рассмотрим некоторый неопределенный параметр 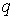 , который может соответствовать вероятности, стоимости, времени или другому показателю. Для описания параметра
, который может соответствовать вероятности, стоимости, времени или другому показателю. Для описания параметра 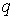 с помощью теории нечетких множеств этот параметр необходимо преобразовать к нечеткому числу
с помощью теории нечетких множеств этот параметр необходимо преобразовать к нечеткому числу  , т.е. задать функцию принадлежности.
, т.е. задать функцию принадлежности.
В настоящем разделе предлагается два способа формирования функций принадлежности: трапециевидный и треугольный. Они позволяют использовать следующую экспертную информацию параметре:
· название параметра 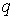 ;
;
· диапазон 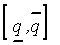 изменения значений параметра
изменения значений параметра 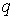 ;
;
· количество лингвистических термов, с помощью которых оценивается параметр 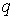 ;
;
· название каждого лингвистического терма.
Определение 4.1. Трапециевидной формой нечеткого числа  (неопределенного параметра
(неопределенного параметра 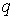 ) будем называть четверку:
) будем называть четверку:
 (4.1)
(4.1)
где 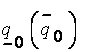 - нижняя (верхняя) граница нечеткого числа
- нижняя (верхняя) граница нечеткого числа  на нулевом
на нулевом  -уровне;
-уровне;
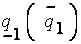 - нижняя (верхняя) граница нечеткого числа
- нижняя (верхняя) граница нечеткого числа  на единичном
на единичном  -уровне;
-уровне;
Интервал 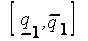 будем называть оптимистической оценкой параметра
будем называть оптимистической оценкой параметра 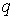 , а интервал
, а интервал 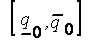 - пессимистической оценкой параметра
- пессимистической оценкой параметра 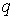 .
.
Такое представление соответствует функции принадлежности, показанной на рис.4.1, которая имеет следующий вид:
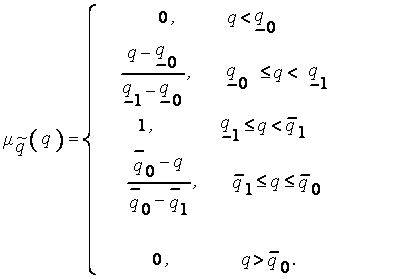 (4.2)
(4.2)
В этом случае носителем нечеткого числа  будет интервал
будет интервал 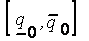 , а ядром -
, а ядром -  .
.
Предложение 4.1. Если нечеткое число  задано в трапециевидной форме
задано в трапециевидной форме  , то переход к
, то переход к  -уровневому описанию
-уровневому описанию
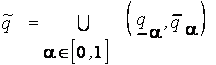
осуществляется по формулам:
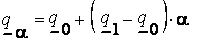 (4.3)
(4.3)
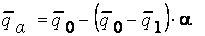 (4.4)
(4.4)

Рис. 4.1. Нечеткое число  с трапециевидной функцией
с трапециевидной функцией
принадлежности
Доказательство. Для перехода к  -уровневому описанию необходимо определить значение нечеткого числа
-уровневому описанию необходимо определить значение нечеткого числа  на любом
на любом  -уровне, т.е. найти такие
-уровне, т.е. найти такие 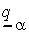 и
и 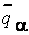 , что
, что
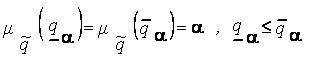 ,
,
где 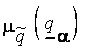 и
и 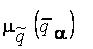 - степени принадлежности элементов
- степени принадлежности элементов 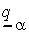 и
и 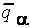 нечеткому множеству
нечеткому множеству  , соответственно.
, соответственно.
Учитывая аналитический вид трапециевидной функции принадлежности (4.2) и подставляя 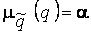 , получаем:
, получаем:
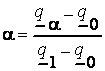 ;
; 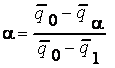 .
.
Отсюда следует, что
 ,
, 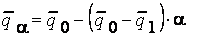 ,
, 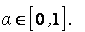
Пример 4.1. Пусть вероятность (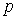 ) безошибочного выполнения операции равна "около 0.9". Требуется задать эту информацию в виде нечеткого числа
) безошибочного выполнения операции равна "около 0.9". Требуется задать эту информацию в виде нечеткого числа 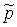 с трапециевидной функцией принадлежности.
с трапециевидной функцией принадлежности.
Решение. Согласно определению 4.1, число 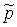 представим в следующем виде:
представим в следующем виде:

где [0.8, 1] - пессимистическая оценка параметра 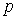 ;
;
[0.85, 0.95] - оптимистическая оценка параметра 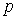 .
.
Разложение нечеткого числа 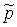 по
по  -уровневым множествам имеет вид:
-уровневым множествам имеет вид:
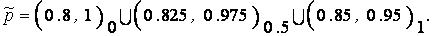
Пример 4.1 иллюстрируется на рис. 4.2,

Рис. 4.2. К примеру 4.1
Определение 4.2. Треугольной формой нечеткого числа  будем называть тройку вида:
будем называть тройку вида:
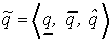 (4.5)
(4.5)
где  - нижняя (верхняя) граница нечеткого числа
- нижняя (верхняя) граница нечеткого числа  на нулевом
на нулевом  -уровне;
-уровне;
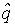 - значение нечеткого числа
- значение нечеткого числа  на единичном
на единичном  -уровне.
-уровне.
Такое описание соответствует функции принадлежности, показанной на рис.4.3, которая имеет следующий аналитический вид:

Носителем нечеткого числа  в этом случае является интервал
в этом случае является интервал 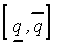 , а ядром, - число
, а ядром, - число 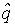 . Интервал
. Интервал 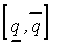 будем называть пессимистической оценкой, а число
будем называть пессимистической оценкой, а число 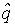 , - оптимистической оценкой параметра
, - оптимистической оценкой параметра 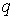 .
.

Рис. 4.3. Нечеткое число  с треугольной функцией принадлежности
с треугольной функцией принадлежности
Предложение 4.2. Если нечеткое число  задано в треугольной форме
задано в треугольной форме 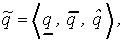 то переход к
то переход к  -уровневому описанию
-уровневому описанию
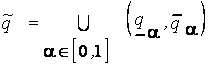
осуществляется по формулам:
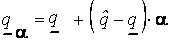 ;
; 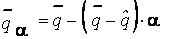 .
.
Доказательство. Треугольная форма неопределенного параметра является частным случаем трапециевидной формы при 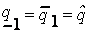 . Подставляя
. Подставляя 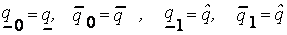 в формулы (4.3) и (4.4), получаем:
в формулы (4.3) и (4.4), получаем:
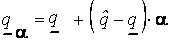 ;
; 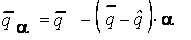 .
.
Пример 4.2. Пусть время ( ) выполнения операции составляет " около 2 сек ". Требуется представить эту информацию в виде нечеткого числа
) выполнения операции составляет " около 2 сек ". Требуется представить эту информацию в виде нечеткого числа 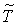 с треугольной формой функции принадлежности.
с треугольной формой функции принадлежности.
Решение. Согласно определению 4.2, нечеткое число 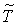 представим в следующем виде:
представим в следующем виде:
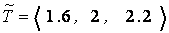 ,
,
где [1.6, 2.2] и 2 - пессимистическая и оптимистическая оценки, соответственно, которые предполагаются известными.
Разложение числа  по
по  -уровневым множествам имеет вид:
-уровневым множествам имеет вид:
 .
.
Пример 4.2 иллюстрируется на рис. 4.4.

Рис. 4.4. К примеру 4.2 Рис. 4.5. Пример функций
принадлежности для 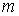 термов
термов
Определение 4.3. l-формой неопределенного параметра 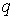 (нечет-кого числа
(нечет-кого числа  ) будем называть тройку вида:
) будем называть тройку вида:
 (4.7)
(4.7)
где 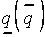 - нижняя (верхняя) граница изменения параметра
- нижняя (верхняя) граница изменения параметра 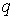 ;
;
l - лингвистическая оценка параметра 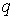 диапазоне
диапазоне 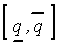 , причем
, причем 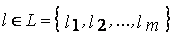 .
.
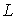 - линейно-упорядоченное по принципу от "меньшего" к "большему" множество лингвистических термов для качественной оценки параметра
- линейно-упорядоченное по принципу от "меньшего" к "большему" множество лингвистических термов для качественной оценки параметра 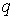 (рис.4.5).
(рис.4.5).
Допущение 4.1. При переходе от l -формы (4.7) нечеткого числа  к трапециевидной форме (4.1) будем предполагать, следующее:
к трапециевидной форме (4.1) будем предполагать, следующее:
(1) носителем нечеткого числа  является интервал
является интервал 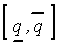 ;
;
(2) размер ядра 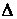 нечетного числа
нечетного числа  зависит oт мощности (
зависит oт мощности (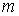 ) терм-множества
) терм-множества 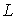 , носителя
, носителя 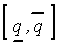 и не зависит от лингвистической переменной;
и не зависит от лингвистической переменной;
(3) для любых соседних термов 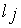 и
и 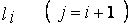 :
:
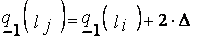 ,
,
где 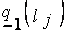 и
и 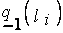 - нижние границы ядра нечеткого числа
- нижние границы ядра нечеткого числа  , выраженного лингвистическими оценками
, выраженного лингвистическими оценками 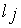 и
и 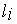 , соответственно;
, соответственно;
(4) для первого терма 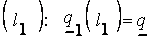 ;
;
(5) для последнего терма 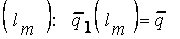 ;
;
Предложение 4.3. Если неопределенный параметр 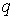 задан
задан 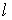 -формой нечеткого числа
-формой нечеткого числа 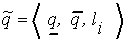 , где
, где 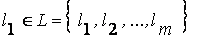 , то переход от
, то переход от 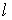 -формы к трапециевидной форме (4.1) осуществляется по формулам:
-формы к трапециевидной форме (4.1) осуществляется по формулам:
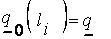 (4.8)
(4.8)
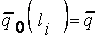 (4.9)
(4.9)
 (4.10)
(4.10)
 (4.11)
(4.11)
где 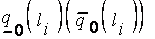 - нижняя (верхняя) граница носителя нечеткого числа
- нижняя (верхняя) граница носителя нечеткого числа  , оцениваемого лингвистическим термом
, оцениваемого лингвистическим термом 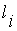 ;
;
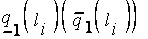 - нижняя {верхняя) граница ядра нечеткого числа
- нижняя {верхняя) граница ядра нечеткого числа  , оцениваемого лингвистическим термом
, оцениваемого лингвистическим термом 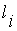 .
.
Доказательство. Из допущения 4.1(1) следует, что для любого лингвистического терма 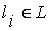 :
:
 и
и  .
.
Учитывая, что размер ядра нечеткого числа определяется по формуле 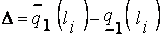 , и, опираясь на допущения 4.1(2)-4.1(5), получаем, что в интервал
, и, опираясь на допущения 4.1(2)-4.1(5), получаем, что в интервал 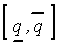 попадает ровно (2
попадает ровно (2 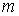 -1) отрезков длиной
-1) отрезков длиной 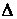 .
.
Отсюда,  . С учетом этого получаем:
. С учетом этого получаем:
для первого терма 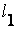 :
:
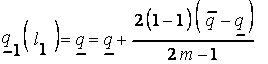 ;
;
 ;
;
для второго терма  :
:
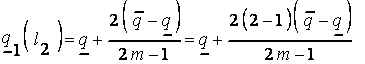
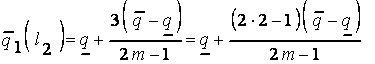 ;
;
для последнего терма 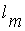 :
:
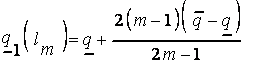 ;
;
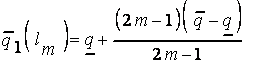 .
.
Отсюда для любого терма 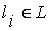 :
:
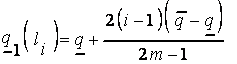 ;
;
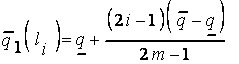 .
.
Предложение 4.3 иллюстрируется рис.4.6.

Рис. 4.6. Переход от 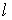 -формы нечеткого числа к трапециевидной форме
-формы нечеткого числа к трапециевидной форме
в случае 4-х термов
Пример 4.3. Пусть вероятность обнаружения ошибок при визуальном контроле задана в виде 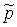 =<0.3, 0.8, выше средней >. При этом используется множество лингвистических оценок:
=<0.3, 0.8, выше средней >. При этом используется множество лингвистических оценок:
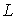 = { низкая, ниже средней, средняя, выше средней, высокая }.
= { низкая, ниже средней, средняя, выше средней, высокая }.
Необходимо представить число 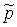 в трапециевидной форме.
в трапециевидной форме.
Решение. Количество лингвистических термов (мощность множества 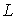 ) равно
) равно 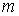 =5. Лингвистическая оценка " выше средней " в множестве
=5. Лингвистическая оценка " выше средней " в множестве 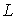 имеет порядковый номер
имеет порядковый номер  =4. Применяя формулы (4.8)-(4.11) из предложения 4.3, получаем:
=4. Применяя формулы (4.8)-(4.11) из предложения 4.3, получаем:
 ;
;
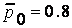 ;
;
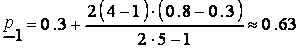 ;
;
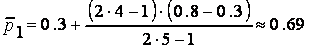 .
.
Поэтому в трапециевидной форме:
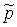 =<0.3, 0.8, 0.63, 0.69>,
=<0.3, 0.8, 0.63, 0.69>,
или в виде разложения по  -уровневым множествам:
-уровневым множествам:
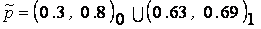 .
.
Графическое изображение нечеткого числа 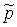 представлено на рис.4.7.
представлено на рис.4.7.

Рис. 4.7. К примеру 4.3
Допущение 4.2. При переходе от 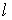 -формы нечеткого числа
-формы нечеткого числа  (4.7) к треугольной форме (4.5) будем предполагать следующее:
(4.7) к треугольной форме (4.5) будем предполагать следующее:
· носителем нечеткого числа  является интервал
является интервал 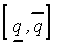 ;
;
· для первого терма 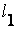 :
:  ;
;
· для последнего терма 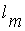 :
:  ;
;
· для соседних термов 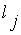 и
и 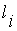 (
(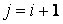 ) расстояние между ядрами
) расстояние между ядрами 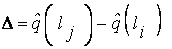 является постоянной величиной,
является постоянной величиной,
где 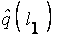 ,
,  ,
, 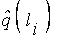 ,
,  - ядра нечеткого числа
- ядра нечеткого числа  соответствующие термам
соответствующие термам 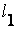 ,
, 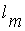 ,
, 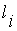 ,
, 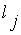 .
.
Предложение 4.4. Если неопределенный параметр 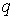 задан
задан 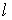 -формой нечеткого числа, где
-формой нечеткого числа, где  , где
, где 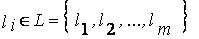 , то переход от
, то переход от 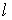 -формы нечеткого числа к треугольной форме (4.5) осуществляется по формулам:
-формы нечеткого числа к треугольной форме (4.5) осуществляется по формулам:
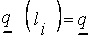 (4.12)
(4.12)
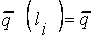 (4.13)
(4.13)
 (4.14)
(4.14)
где 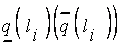 - нижняя (верхняя) граница носителя нечеткого числа
- нижняя (верхняя) граница носителя нечеткого числа  , выраженного лингвистической оценкой
, выраженного лингвистической оценкой 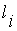 ;
;
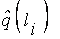 - ядро нечеткого числа
- ядро нечеткого числа  , выраженного лингвистической оценкой
, выраженного лингвистической оценкой 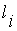 .
.
Доказательство этого предложения аналогично тому, которое| использовалось в предложении 4.3. Предложение 4.4 иллюстрирует рис.4.8.
Пример 4.4. Пусть информация о времени выполнения контрольной операции задана 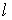 -формой нечеткого числа:
-формой нечеткого числа:
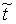 = < 10, 19, высокое >.
= < 10, 19, высокое >.
Множество лингвистических оценок имеет вид:
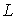 = { низкое, среднее, высокое, очень высокое }.
= { низкое, среднее, высокое, очень высокое }.
Требуется представить число 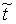 в треугольной форме.
в треугольной форме.
Решение. Количество лингвистических термов (мощность множества 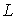 ) равно четырем. Лингвистическая оценка < высокое > в множестве
) равно четырем. Лингвистическая оценка < высокое > в множестве 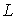 имеет порядковый номер
имеет порядковый номер  =3. Применяя формулы (4.12)-(4.14), получаем:
=3. Применяя формулы (4.12)-(4.14), получаем:
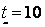 ;
; 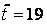 ;
;
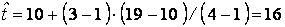 .
.
Окончательно находим:
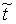 =< 10, 19. 16 >.
=< 10, 19. 16 >.
Функция принадлежности нечеткого числа 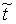 показана на рис.4.9.
показана на рис.4.9.
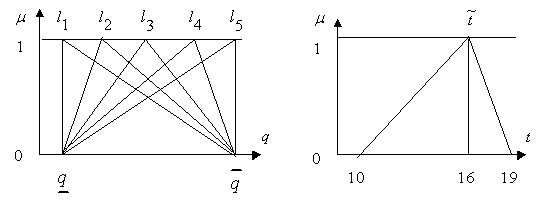
Рис. 4.8. Переход от 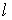 -формы к треугольной в случае пяти термов
-формы к треугольной в случае пяти термов
Рис. 4.9. К примеру 4.4
Не нашли, что искали? Воспользуйтесь поиском: