Применение композиционного правила вывода

Постановка задачи

Будем считать известными:

· множество решений -классов в рассматриваемой предметной области;

· функции принадлежности, позволяющие представлять каждый класс 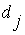, в виде нечеткого множества (3.9);

· множество параметров состояния объекта , влияющих на решение;

· множества лингвистических термов для качественной оценки параметров , , т.е.

...

...

· функции принадлежности, позволяющие представлять качественные термы параметров , в виде нечетких множеств (3.8);

· матрицу знаний (табл. 3.1).

Требуется разработать алгоритм принятия решения, позволяющий фиксированному множеству

, ,..., .

качественных оценок параметров состояния конкретного объекта поставить в соответствие решение-класс (рис. 3.2).

Идея алгоритма, который разрабатывается ниже для решения этой задачи, состоит в использовании композиционного правила вывода Заде [15], устанавливающего связь между одной входной и одной выходной переменными. Это правило обобщается ниже на случай одного выхода и входов, что соответствует полной матрице знаний (табл. 3.1).

Не нашли, что искали? Воспользуйтесь поиском: