
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Функции принадлежности
По определению [15], функция принадлежности 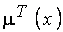 характеризует субъективную меру (в диапазоне [0,1]) уверенности эксперта в том, что четкое значение
характеризует субъективную меру (в диапазоне [0,1]) уверенности эксперта в том, что четкое значение  соответствует нечеткому терму
соответствует нечеткому терму  . Наибольшее распространение в практических приложениях [84] получили треугольные, трапециевидные и колоколообразные (гауссовы) функции принадлежности, параметры которых позволяют менять форму функций.
. Наибольшее распространение в практических приложениях [84] получили треугольные, трапециевидные и колоколообразные (гауссовы) функции принадлежности, параметры которых позволяют менять форму функций.
Нами предлагается простая и удобная для настройки аналитическая модель функций принадлежности переменной  произвольному нечеткому терму
произвольному нечеткому терму  в виде:
в виде:
 (3.12)
(3.12)
где 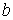 и
и  -параметры настройки:
-параметры настройки: 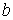 - координата максимума функции,
- координата максимума функции,  ;
;  - коэффициент концентрации - растяжения функции (рис. 3.1). Для нечеткого терма
- коэффициент концентрации - растяжения функции (рис. 3.1). Для нечеткого терма  число
число 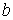 представляет наиболее возможное значение переменной
представляет наиболее возможное значение переменной  .
.

Не нашли, что искали? Воспользуйтесь поиском: