Объекты с непрерывным выходом

Разобьем интервал , на котором изменяется выход 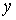объекта, на 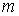частей:

(3.14)

Известную экспертную информацию про объект с непрерывным выходом зададим в виде системы нечетких логических высказываний:

ЕСЛИ

ИЛИ (3.15)

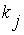где - лингвистический терм, которым оценивается переменная в строчке с номером ; - количество строчек - конъюнкций, соответствующих интервалу , .

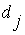Постановка задачи

Будем считать известными:

· интервал изменения выходной переменной ,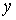

· множество входных переменных ,

· диапазоны количественного изменения каждой входной переменной , ,

· функции принадлежностей, позволяющие представлять переменные , в виде нечетких множеств (3.6) или (3.8),

· система логических высказываний вида (3.15), которая может быть представлена в виде матрица знаний из раздела 3.1.3.

Требуется: разработать алгоритм принятия решения, позволяющий фиксированному вектору входных переменных , поставить в соответствие решение .

Алгоритм нечеткого логического вывода, приведенный в разделе 3.2.3 позволяет вычислить выходную величину 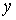в виде нечеткого множества:

(3.16)

Для получения четкого числа из интервала , соответствующего нечеткому значению (3.16), необходимо применить операцию дефаззификации. Дефаззификация (от англ. defuzzification [85]) - это операция преобразования нечеткой (fuzzy) информации в четкую форму. Определим четкое число , которое соответствует нечеткому множеству (3.16), таким образом:

(3.17)

При вероятностной интерпретации степеней принадлежности, формула (3.17) может рассматриваться как аналог математического ожидания дискретной случайной величины.

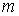Если интервал разбить на равных частей, то есть

, ,..., , ,

то формула (3.17) упрощается и принимает вид, удобный для расчетов:

(3.18)

Не нашли, что искали? Воспользуйтесь поиском: