Принцип обобщения Заде

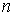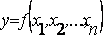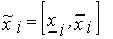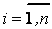Определение 4.6. Если задана функция от переменных и аргументы - суть нечеткие числа с носителями supp , то нечеткое число определяется следующим образом [6,15]:

(4.16)

Реализация этого принципа осуществляется по следующему алгоритму.

I°. Зафиксировать значение .

2°.Найти все 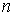-ки 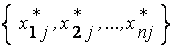, удовлетворяющие условиям:

, , , .

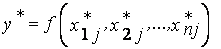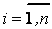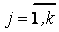3°.Степень принадлежности элемента 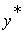нечеткому числу 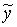определить по формуле:

.

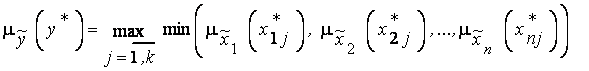4°. Проверить условие "Взяты все элементы 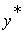?". Если "да", то перейти к шагу 5, иначе зафиксировать новое значение 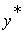и перейти к шагу 2.

5°. Конец.

Пример 4.6. Пусть заданы нечеткие числа

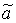=0/1+1/2+1/3+0/4 и =0/2+1/3+1/4+0/8.

Требуется найти нечеткое число с использованием принципа обобщения.

Решение. Процесс решения сведен в табл.4.1. Из этой таблицы видно, что нечеткое число 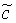определяется так:

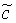=0/2+ 0/3 + 0/4 + 1/6 + 1/8 +1/9 + 1/12 + 0/16 + 0/24 +0/32.

Переходя к разложениям по -уровневым множествам, получаем:

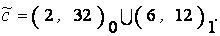
В этом примере применение принципа обобщения Заде потребовало перебора 16 вариантов.

Таблица 4.1 к примеру 4.6

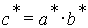
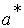
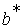
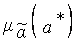
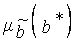
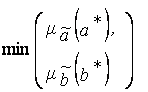
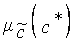
Предложение 4.5. Если 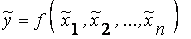- функция от 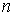нечетких аргументов 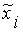, каждый из которых задается функцией принадлежности в точках универсального множества

,

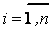
тo для определения нечеткого числа 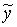по принципу обобщения Заде необходимо перебрать 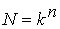вариантов.

Доказательство этого предложения следует из элементарных комбинаторных рассуждений.

Из предложения 4.5 становится ясно, что применение известного принципа обобщения Заде [6,15] связано с большими вычислительными трудностями. Например, для нахождения только одного значения функции от семи аргументов (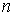 = 7), каждый из которых задан на трех -уровнях (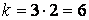), необходимо перебрать = 6⁷ = 279 936 вариантов.

Для решения практических задач ниже будет предложен модифицированный принцип обобщения, не требующий трудоемких вычислительных процедур. Для доказательства его корректности введем -уровневый принцип обобщения.

4.3.2. -уровневый принцип обобщения

Определение 4.7. Если задана функция от нечетких аргументов 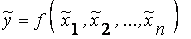, в которой нечеткие числа представлены в виде разложения по -уровневым множествам:

, , .

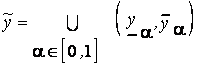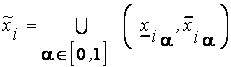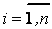то для любого -уровня значение функции вычисляется по формулам:

;

,

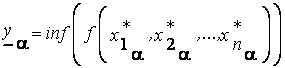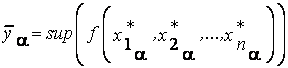где , .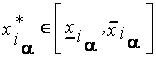

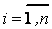Эквивалентность -уровневого принципа обобщения и классического принципа обобщения Заде доказывается в следующем предложении.

Предложение 4.6. Если задана функция от нечетких аргументов 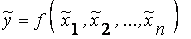и нечеткие числа представлены в виде разложения по -уровневым множествам:

, , .

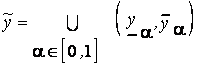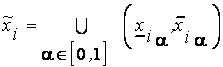то результаты нечеткого обобщения по определениям 4.6 и 4.7 совпадают.

Доказательство. Достаточно доказать, что определение 4.7 следует из определения 4.6. Вначале покажем, что для вычисления значения функции 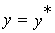на конкретном -уровне достаточно знать значения аргументов только на этом -уровне. В этом случае формула (4.16) преобразуется к виду:

(4.17)

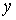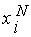Докажем, что применение значений аргументов на других -уровнях не добавляет новых значений со степенью принадлежности . Доказательство выполним от противного. Рассмотрим аргумент . Новое значение аргумента обозначим через . Предположим, что изменение аргумента добавит новое значение 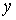со степенью принадлежности . Возможны следующие три случая:

Случаи 1: и .

В связи с тем, что нечеткие числа представлены в виде разложения по -уровневым множествам, то из выполнения условия

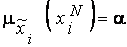следует, что 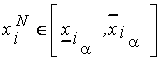Последнее означает, что аргумент 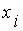не изменяется. Поэтому новые значения 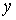со степенью принадлежности не появляются.

Случай 2: и .

Первое условие означает, что диапазон изменения 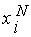шире, чем . В связи с этим . В результате расширения диапазона изменения аргумента 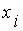может появиться новое значение 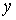. Однако это новое значение 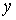не может иметь степень принадлежности равную , т.к. по формуле (4.16) .

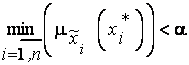Таким образом, изменение аргумента не приводит к появлению новых значений 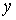со степенью принадлежности .

Случай 3: 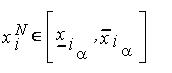и

Первое условие означает, что диапазон изменения аргумента не расширился. Учитывая второе условие, получаем . Отсюда следует, что диапазон изменения аргумента сузился, что означает невозможность появления новых значений .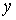

Таким образом, любое изменение аргумента 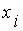не приводит к появлению новых значений 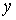со степенью принадлежности равной . Аналогичные выкладки можно проделать для всех остальных аргументов. Это означает, что в случае представления нечетких чисел в виде разложения по - уровневым множествам формула (4.17) справедлива.

Заметим, что

.

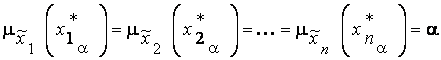Поэтому результат применения операций min и sup в (4.17) всегда равен . Формула (4.17) дает ряд значений со степенью принадлежности, равной . Для перехода к -уровневому представлению необходимо найти минимальное и максимальное значения:

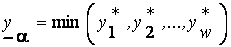и

Окончательно получаем:

;

,

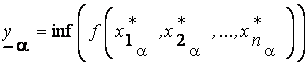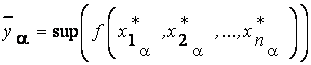где , , .

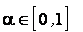Применение -уровневого принципа обобщения сопряжено с необходимостью решения задачи оптимизации, которая формулируется следующим образом.

Дано: функция от 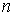переменных 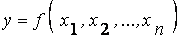, в которой аргументы , .

Требуется: найти такие значения аргументов , которые обеспечивают максимальное и минимальное 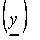значение функции 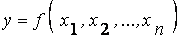на области определения , .

В общем случае решение этой задачи является достаточно сложным. Однако, вводя ряд ограничений, свойственных peальным моделям, удается упростить решение оптимизационной задачи и получить достаточно простой алгоритм.

Не нашли, что искали? Воспользуйтесь поиском: