
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Выражение тригонометрических функций через тангенс половинного угла
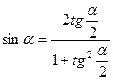 ,
, 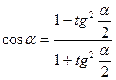 ,
,
,.
Преобразование степеней синуса и косинуса
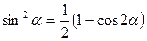 ,
,
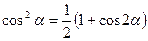 ,
,
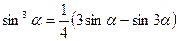 ,
,
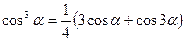 ,
,
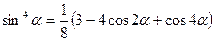 ,
,
.
1(А). Найти  , если
, если  и
и  .
.
2(А). Вычислить 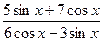 , если
, если 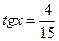 .
.
3(В). Вычислить 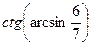 .
.
4(А). Найти  , если выполняется равенство
, если выполняется равенство 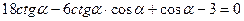 .
.
5(В). Вычислить 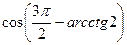 .
.
6(А). Упростить 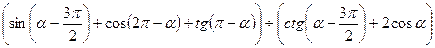 .
.
7(В). Найти 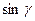 , если
, если 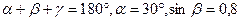 и
и 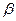 - тупой угол.
- тупой угол.
8(А). Доказать, что  , если
, если  ,
, 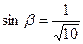 и
и  - острые углы.
- острые углы.
9(А). Найти 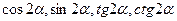 , если
, если 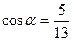 и
и 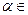 I четверти.
I четверти.
10(В). Вычислить 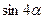 , если
, если  .
.
11(В). Вычислить  , если
, если 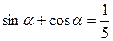 .
.
12(В). Вычислить  .
.
13(В). Вычислить 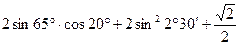 .
.
14(В). Если 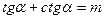 , тогда
, тогда  ,
, 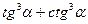 ,
, 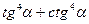 выразите через
выразите через  .
.
15(А). Докажите тождества 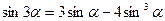 ,
, 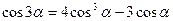 .
.
16(В). Найдите  , если
, если 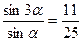 .
.
17(В). Вычислите 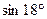 .
.
18(А). Решите уравнение 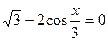 .
.
19(В). Найдите сумму (в градусах) двух самых больших корней уравнения 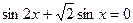 , принадлежащих промежутку
, принадлежащих промежутку 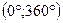 .
.
20(В). Найдите сумму (в градусах) корней уравнения 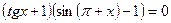 , принадлежащих интервалу
, принадлежащих интервалу  .
.
21(В). Укажите количество корней уравнения 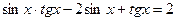 , принадлежащих отрезку
, принадлежащих отрезку  .
.
22(В). Укажите количество корней уравнения 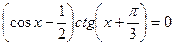 , принадлежащих отрезку
, принадлежащих отрезку  .
.
23(В). Укажите количество корней уравнения 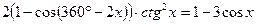 , принадлежащих отрезку
, принадлежащих отрезку  .
.
24(В). Укажите количество корней уравнения 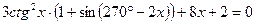 , принадлежащих отрезку
, принадлежащих отрезку 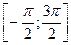 .
.
25(В). Найдите сумму (в градусах) корней уравнения  , принадлежащих отрезку
, принадлежащих отрезку  .
.
26(В). Найдите сумму двух последовательных целых чисел, между которыми находится корень уравнения  .
.
27(В). Решите уравнения:


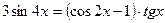
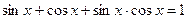
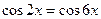
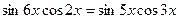
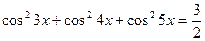
28(В). Решить уравнения:
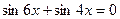
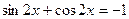
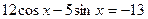

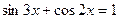

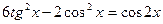
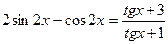
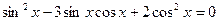
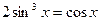
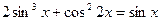
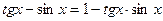 .
.
29(В). Вычислите 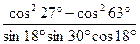 .
.
30(В). Вычислить 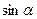 , если
, если 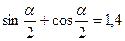 .
.
31(В). Вычислить 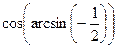 ;
;  ;
;  ;
;  ;
;  .
.
32(В). Зная, что 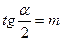 , найти
, найти 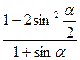 .
.
33(В). Найдите наибольшее и наименьшее значения функции 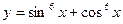 .
.
34(В). Найдите множество значений функций:  ;
; 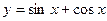 .
.
35(В). Найдите произведение двух последовательных целых чисел, между которыми находится число 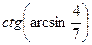 .
.
36(В). Найдите произведение наибольшего и наименьшего значений функции 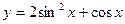 .
.
37(С). Найдите значение параметра 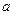 (или произведение таких значений, если их несколько), при которых основной период функции
(или произведение таких значений, если их несколько), при которых основной период функции  равен
равен 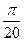 .
.
39(С). Найдите значение параметра 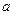 (или произведение таких значений, если их несколько), при которых основной период функции
(или произведение таких значений, если их несколько), при которых основной период функции 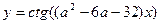 равен
равен 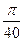 .
.
40(С). Найдите число корней уравнения 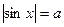 , принадлежащих отрезку
, принадлежащих отрезку  .
.
41(В). Найти 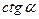 , если выполняется равенство:
, если выполняется равенство: 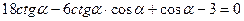 .
.
42(В). Вычислить 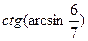 .
.
43(В). Вычислить 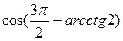 .
.
44(А). Вычислить  .
.
45(А). Упростить 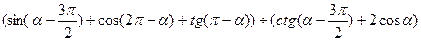 .
.
46(В). Доказать справедливость тождеств:
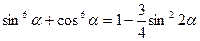
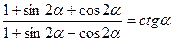
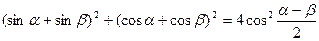
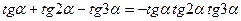

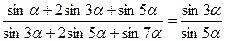
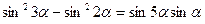
47(В). Решить уравнения
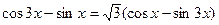
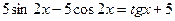
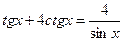
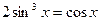
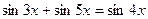

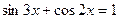

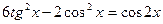
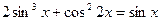
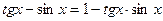
| 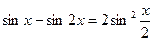

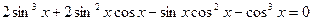
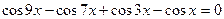
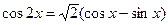
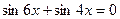
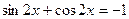
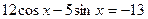
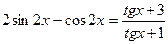
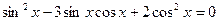
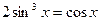
|
48(С). Решить задачи:
* Найдите произведение целых значений функции 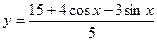 .
.
* Найдите 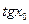 , где
, где  - наименьший, положительный корень уравнения
- наименьший, положительный корень уравнения 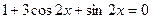 .
.
*Вычислите 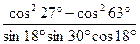 .
.
* Найдите основной период функции 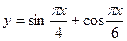 .
.
* Найдите целое решение (или сумму целых решений, если их несколько) неравенства 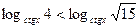 на промежутке
на промежутке 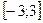 .
.
* Определите число корней уравнения 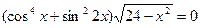 .
.
* Найдите число точек разрыва функции 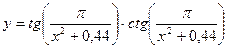 .
.
* Найдите корень, принадлежащий отрезку 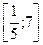 , (или произведение корней, если их несколько) уравнения
, (или произведение корней, если их несколько) уравнения 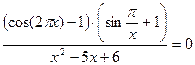 .
.
* Найдите значение выражения 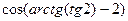 .
.
* Найдите целое решение (или сумму целых решений, если их несколько) неравенства 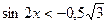 на промежутке
на промежутке  .
.
* Найдите корень (или сумму корней, если их несколько) уравнения  , принадлежащих отрезку
, принадлежащих отрезку 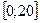 .
.
* Найдите число корней уравнения 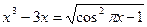 .
.
* Найдите значение параметра 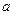 (или произведение таких значений, если их несколько), при которых основной период функции
(или произведение таких значений, если их несколько), при которых основной период функции 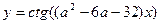 равен
равен 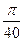 .
.
* Найдите положительный корень (или сумму таких корней, если их несколько) уравнения 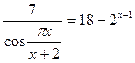 .
.
Текстовые задачи
1. Из пункта А в пункт В, расстояние между которыми равно 84 км, выехал велосипедист, а через 2 ч навстречу ему из В в А выехал мотоциклист, скорость которого на 48 км/ч больше скорости велосипедиста. Найти их скорости, если известно, что к моменту встречи велосипедист проехал на 16 км меньше, чем мотоциклист.
2. Два поезда вышли из города А в город В, и весь путь каждый из поездов прошел с постоянной скоростью. Второй поезд вышел на 5 ч позже первого и прибыл в В одновременно с первым поездом. За один час до прибытия в В расстояние между поездами составило 30 км, а когда первый поезд находился в середине пути, то второй отставал от него на 225 км. Найти скорости поездов и расстояние между городами.
3. Поезд должен был пройти 54 км. Пройдя 14 км, он был задержан у семафора на 10 мин. Увеличив скорость после этого на 10 км/ч, он прибыл на место назначения с опозданием на 2 мин. Определить первоначальную скорость поезда.
4. Расстояние от А до В по течению моторная лодка проплывает за 8 ч, а от В до А против течения – за 12 ч. За сколько часов проплывает расстояние от А до В плот? Скорость плота равна скорости течения.
5. Дорога от А до В длиной 11,5 км идет сначала в гору, потом по ровному месту и затем под гору. Пешеход, идя из А в В, прошел всю дорогу за 2 ч 54 мин, а на обратную дорогу затратил 3 ч 6 мин. Скорость ходьбы: в гору 3 км/ч, по ровному месту 4 км/ч, под гору 5 км/ч. На каком протяжении дорога идет по ровному месту?
6. Два подъемных крана разгрузили баржу за 40 ч совместной работы. Если бы половину баржи разгрузил один кран, а затем другую половину – второй, то на разгрузку баржи ушел бы 81 ч. За сколько времени может разгрузить баржу каждый кран, работая один?
7. Два тракториста при совместной работе обрабатывают поле за 45 мин. Сколько времени потребовалось бы одному первому трактористу на обработку поля, если известно, что один второй тракторист обрабатывает все поле на 2 ч дольше, чем первый?
8. Три рабочих, работая вместе, могут выполнить всю работу за  ч. Первый может выполнить эту работу вдвое быстрее второго и на 1 ч быстрее третьего. За какое время каждый рабочий может выполнить эту работу?
ч. Первый может выполнить эту работу вдвое быстрее второго и на 1 ч быстрее третьего. За какое время каждый рабочий может выполнить эту работу?
9. Два каменщика, работая вместе, могут выполнить задание за 12ч. Производительность труда первого и второго каменщиков относятся как 1:3. Каменщики договорились работать поочередно. Сколько времени должен проработать первый каменщик, чтобы это задание было выполнено за 20 ч?
10. Два раствора, из которых первый содержит 0,8 кг, а второй 0,6 кг безводной серной кислоты, соединили вместе и получили 10 кг раствора серной кислоты. Найти массу первого и второго растворов, вошедших в смесь, если известно, что в первом растворе безводной серной кислоты содержится на 10% больше, чем во втором растворе.
11. Имеется два различных сплава меди. Процент содержания меди в первом сплаве на 40 меньше, чем во втором сплаве. После того как их сплавили вместе, получили сплав, содержащий 36% меди. Определить процентное содержание меди в первом и втором сплавах, если известно, что меди в первом сплаве 6 кг, а во втором 12 кг.
12. 800 кг руды содержат некоторое количество железа. После удаления из руды 400 кг примесей, содержащих 12,5% железа, процент содержания железа в оставшейся руде повысился на 25%. Определить, сколько кг железа содержится в 800 кг руды.
13. К раствору, содержащему 40 г соли, добавили 200г воды, после чего концентрация уменьшилась на 10%. Сколько воды содержал раствор?
14. Найти двузначное число, если известно, что сумма квадратов его цифр равна 53, а сумма его цифр в три раза меньше искомого числа.
15. Трехзначное число оканчивается цифрой 3. Если эту цифру перенести влево (т.е. поставить в начале), то новое число будет на 1 больше утроенного первоначального числа. Найти это число.
16. В двух колоннах, состоящих из 28 автомобилей в каждой, было 11 «Жигулей», остальные – «Москвичи». Сколько «Москвичей» было в каждой колонне, если известно, что в первой из них на каждую машину «Жигули» приходилось в два раза больше «Москвичей», чем во второй?
17. Найдите двузначное число (или сумму таких двузначных чисел, если их несколько), которое при перестановке цифр местами уменьшается на 28,125%.
18. В течение года завод дважды увеличивал выпуск продукции на одно и то же число процентов. Найти это число, если известно, что в начале года завод ежемесячно выпускал 600 изделий, а в конце года стал выпускать ежемесячно 726 изделий.
19. Вкладчику на его сберкнижку за год сберкасса начислила 6 р. процентных денег. Добавив 44 р., вкладчик оставил деньги еще на год. По истечении года вновь было произведено начисление процентов, и теперь вклад вместе с процентами составил 257 р. 50 к. Какая сумма первоначально была положена на сберкнижку, и был ли этот вклад обыкновенным (2%-ным) или срочным (3%-ным)?
20. После двух последовательных снижений цен на одно и то же число процентов цена товара снизилась с 25 р. до 16 р. На сколько процентов снижалась цена товара каждый раз?
21. Периметр прямоугольного треугольника равен 48 см, а его площадь 96 см  . Найти длины сторон треугольника.
. Найти длины сторон треугольника.
22. Высота прямоугольника составляет 75% его основания. Найти периметр этого прямоугольника, если площадь прямоугольника равна 48 м  .
.
23. От квадратного листа отрезали полосу шириной 3 см, после чего площадь оставшейся части листа стала равной 10 см  . Определить первоначальные размеры листа.
. Определить первоначальные размеры листа.
24. Встречаются две команды шашистов А и Б. По условиям соревнований каждый участник одной команды играет по одной партии с каждым участником другой команды. Общее число предстоящих партий в 4 раза больше числа всех игроков в обеих командах. Однако из-за болезни два игрока не смогли явиться на матч, в связи с чем число всех сыгранных в матче партий оказалось на 17 меньше предполагавшихся. Сколько игроков выступило в матче за команду А, если известно, что в ней было меньше игроков, чем в команде Б.
25. Найти два двузначных числа, обладающих следующим свойством: если к большему искомому числу приписать справа 0 и затем меньшее число, а к меньшему приписать справа большее число и затем 0, то из образовавшихся таким образом двух пятизначных чисел первое, будучи разделенным на второе, дает в частном 2 и в остатке 590. Кроме того, известно, что сумма удвоенного большего искомого числа и утроенного меньшего равна 72.
26. Из сосуда, наполненного 96%-ным раствором кислоты, отлили 2,5 л и долили 2,5 л 80%-ного раствора той же кислоты, затем еще раз отлили 2,5 л и снова долили 2,5 л 80%-ного раствора кислоты. После этого в сосуде получился 89%-ный раствор кислоты. Определить вместимость сосуда.
27. В начале года 5/6 некоторого количества денег положили в первый банк, а оставшуюся часть – во второй банк. К концу года сумма этих вкладов стала равной 670 денежным единицам, к концу следующего года – 749 денежным единицам. Было подсчитано, что если бы первоначально 5/6 исходного количества денег положили во второй банк, а оставшуюся часть – в первый банк, то по истечении одного года сумма этих вкладов стала равной 710 денежным единицам. В предположении, что исходное количество денег первоначально целиком положено в первый банк, определить величину вклада по истечении двух лет.
Прогрессии.
Арифметическая прогрессия – числовая последовательность  , определяемая условиями:
, определяемая условиями:
1) 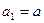 , 2)
, 2) 
(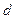 - разность арифметической прогрессии).
- разность арифметической прогрессии).
Свойства арифметической прогрессии:
1. 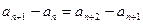 ,
,
2.  .
.
Формула  -го члена:
-го члена:
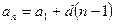 .
.
Формула суммы  первых членов:
первых членов:
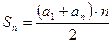 ,
,
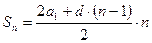
Геометрическая прогрессия – числовая последовательность 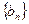 , определяемая условиями:
, определяемая условиями:
1) 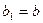
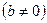 , 2)
, 2) 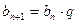
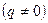
(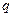 − знаменатель геометрической прогрессии).
− знаменатель геометрической прогрессии).
Свойства геометрической прогрессии:
1. 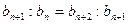 ,
,
2. 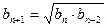
 .
.
Формула  -го члена:
-го члена:
 .
.
Формула суммы  первых членов:
первых членов:
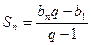 ,
,
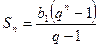 .
.
Сумма бесконечно убывающей геометрической прогрессии  .
.
- В арифметической прогрессии
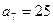 ,
, 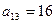 . Найдите количество отрицательных членов прогрессии, каждый из которых не меньше -32.
. Найдите количество отрицательных членов прогрессии, каждый из которых не меньше -32. - В арифметической прогрессии
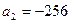 ,
,  . Укажите такое
. Укажите такое  , при котором сумма
, при котором сумма 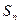 принимает наименьшее возможное значение.
принимает наименьшее возможное значение. - В арифметической прогрессии
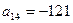 ,
, 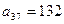 . Укажите номер
. Укажите номер  члена этой прогрессии, начиная с которого все ее члены положительны. Дома.
члена этой прогрессии, начиная с которого все ее члены положительны. Дома. - Сумма первого и пятого членов арифметической прогрессии равна 5/3, а произведение третьего и четвертого ее членов равно 65/72. Найти сумму семнадцати первых членов прогрессии.
- В арифметической прогрессии сумма седьмого и тринадцатого членов равна 5, а разность одиннадцатого и восемнадцатого равна 7. Найдите число членов прогрессии, не превышающих по модулю 50.
- Найти сумму первых девятнадцати членов арифметической прогрессии а1, а2,…, если известно а4 + а8 + а12 + а16 = 224.
- Найдите наибольшую из сумм первых
 членов арифметической прогрессии, если
членов арифметической прогрессии, если  ,
, 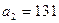 . Дома.
. Дома. - Найти сумму всех четных трехзначных чисел, делящихся на 3. Дома.
- Если первый член геометрической прогрессии равен 2, а четвертый равен -16, то сумма первых шести членов прогрессии равна …
- В знакочередующейся геометрической прогрессии первый член равен 27, а сумма первых трех ее членов равна 39. Найдите третий член прогрессии.
- Найдите сумму значений
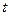 или значение
или значение 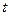 , если оно единственное, при котором числа
, если оно единственное, при котором числа  являются тремя последовательными членами возрастающей геометрической прогрессии
являются тремя последовательными членами возрастающей геометрической прогрессии - Найти первый и пятый члены геометрической прогрессии, если известно, что знаменатель ее равен 3, а сумма шести ее первых членов равна 1820.
- Найдите сумму бесконечно убывающей геометрической прогрессии
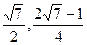 , …
, … - В геометрической прогрессии известны члены
 ,
, 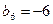 . Укажите номер
. Укажите номер  члена этой прогрессии, начиная с которого все ее члены не больше -48.
члена этой прогрессии, начиная с которого все ее члены не больше -48. - В геометрической прогрессии известны члены
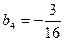 ,
, 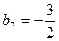 . Укажите номер
. Укажите номер  члена этой прогрессии, начиная с которого все ее члены не больше -384. Дома.
члена этой прогрессии, начиная с которого все ее члены не больше -384. Дома. - В знакочередующейся геометрической прогрессии первый член равен 7, а сумма третьего и пятого членов равна 140. Найдите второй член прогрессии. Дома.
- Если к четырем числам
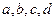 , составляющим геометрическую прогрессию, прибавить соответственно 4, 21, 29 и 1, то получатся 4 числа, составляющие арифметическую прогрессию. Найдите
, составляющим геометрическую прогрессию, прибавить соответственно 4, 21, 29 и 1, то получатся 4 числа, составляющие арифметическую прогрессию. Найдите 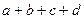 .
.
Производная.
Таблица производных основных элементарных функций.
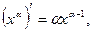

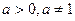 ;
; 
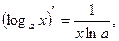
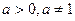 ;
;  ,
,
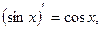

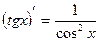 ,
,
 ,
,
 ,
,
 ,
,
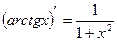 ,
,
.
Правила дифференцирования. Пусть 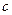 – постоянная,
– постоянная, 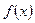 и
и 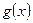 - дифференцируемые функции; тогда
- дифференцируемые функции; тогда
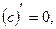
 ,
,
 ,
,
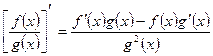 .
.
Теорема о производной сложной функции. Пусть  имеет производную в точке
имеет производную в точке  , а функция
, а функция 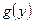 имеет производную в точке
имеет производную в точке 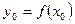 ; тогда сложная функция
; тогда сложная функция 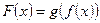 имеет производную в точке
имеет производную в точке  , равную
, равную  .
.
Типовые задачи.
1. Вычислить производную функции:
 ,
,
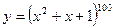 ,
,
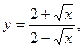
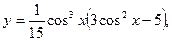
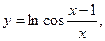
.
2. Исследовать на возрастание и убывание функции:
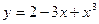 ,
,
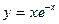 ,
,
.
3. Найти экстремумы следующих функций:

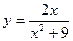 ,
,
.
4. Найти наибольшее и наименьшее значения функции на отрезках:
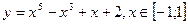 ,
,
 ,
,
.
5. 1. На кривой 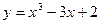 найти точки, в которых касательная параллельна прямой
найти точки, в которых касательная параллельна прямой 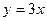 .
.
5.2. Записать уравнение горизонтальной касательной к графику функции 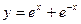 .
.
5.3. Записать уравнение касательной к графику функции 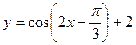 в точке с абсциссой
в точке с абсциссой 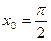 .
.
5.4. Число 18 представить в виде суммы двух положительных слагаемых так, чтобы сумма их квадратов была наименьшей.
5.5. Из всех конусов, вписанных в шар радиуса R, найти тот, у которого площадь боковой поверхности наибольшая.
Тестовые задачи.
1. Найти производную функции 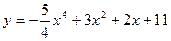 .
.
2. Найдите количество точек экстремума функции  , если ее производная
, если ее производная
 . (Области определения функций
. (Области определения функций 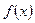 и
и  совпадают.)
совпадают.)
3. Угловой коэффициент касательной к графику функции 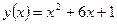 равен -4. Найдите сумму координат точки касания.
равен -4. Найдите сумму координат точки касания.
4. Материальная точка движется по оси OX по закону 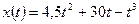 (
( - координата в метрах,
- координата в метрах, 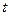 - время в секундах). Через сколько секунд после начала движения точка остановится?
- время в секундах). Через сколько секунд после начала движения точка остановится?
5. Найдите сумму наибольшего и наименьшего значений функции 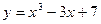 на отрезке
на отрезке 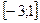 .
.
6. Составьте уравнение касательной к графику функции 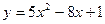 в точке с абсциссой
в точке с абсциссой  .
.
7. Найдите длину промежутка убывания функции  , если ее производная
, если ее производная 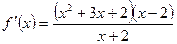 .
.
8. Угловой коэффициент касательной к графику функции 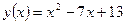 равен значению функции в точке касания. Найдите сумму абсцисс точек касания.
равен значению функции в точке касания. Найдите сумму абсцисс точек касания.
9. Найдите длину промежутка возрастания функции  .
.
10. К графику функции 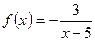 проведены две параллельные касательные, одна из которых проходит через точку А(8;-1), принадлежащую графику функции. Составьте уравнение второй касательной.
проведены две параллельные касательные, одна из которых проходит через точку А(8;-1), принадлежащую графику функции. Составьте уравнение второй касательной.
11. Пусть производная функции 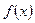 имеет вид
имеет вид 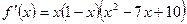 . Найдите суммарную длину промежутков возрастания функции
. Найдите суммарную длину промежутков возрастания функции 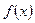 .
.
12. Найдите наименьшее значение функции 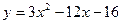 на отрезке
на отрезке 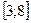 .
.
13. Прямая, проходящая через начало координат, касается графика функции 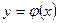 в точке А(6;3). Найдите
в точке А(6;3). Найдите  .
.
14. Найдите точки максимума функции 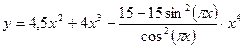 .
.
15. Точка движется по прямой, причем ее пройденный путь определяется формулой
 . Найдите наименьший момент времени, в который скорость точки равна
. Найдите наименьший момент времени, в который скорость точки равна  .
.
16. Найдите сумму координат точки пересечения касательной, проведенной к графику функции  в его точке с абсциссой
в его точке с абсциссой  , с осью абсцисс.
, с осью абсцисс.
17. Найдите сумму наибольшего и наименьшего целых значений функции
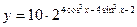 .
.
18. Прямая  касается параболы
касается параболы  в точке с абсциссой
в точке с абсциссой  . Найдите сумму
. Найдите сумму  .
.
19. Уравнение движения точки вдоль оси OX имеет вид:  . В момент времени
. В момент времени  сек. абсцисса точки
сек. абсцисса точки  см., а скорость точки равна 20 см/сек. При
см., а скорость точки равна 20 см/сек. При 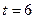 сек. скорость точки равна 32 см/сек. Найдите значение
сек. скорость точки равна 32 см/сек. Найдите значение  .
.
20. Найдите произведение наибольшего и наименьшего значений функции 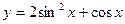 .
.
Геометрия.
Не нашли, что искали? Воспользуйтесь поиском: