
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Кривые второго порядка
Определение. Кривыми второго порядка являются линии, уравнения которых есть уравнения второй степени с двумя неизвестными:
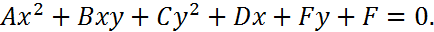
Причем, хотя бы один из коэффициентов 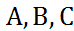 не равен нулю.
не равен нулю.
К кривым второго порядка относятся: окружность, эллипс, гипербола и парабола.
Для задания невырожденной кривой второго порядка (оси которой параллельны координатным осям) необходимо выполнение условий:
1) если 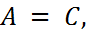 то уравнение определяет окружность;
то уравнение определяет окружность;
2) если 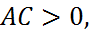 то уравнение определяет эллипс;
то уравнение определяет эллипс;
3) если 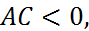 то уравнение определяет гиперболу;
то уравнение определяет гиперболу;
4) если 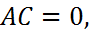 то уравнение определяет параболу.
то уравнение определяет параболу.
Определение. Окружностью радиуса 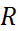 называется множество всех точек
называется множество всех точек 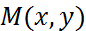 плоскости, равноудаленных от данной точки
плоскости, равноудаленных от данной точки  , называемой центром (см. рис. 5).
, называемой центром (см. рис. 5).
Тогда, можем записать:
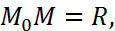

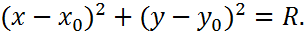 (12)
(12)
Уравнение (12) называется нормальным уравнением окружности.
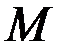
|
| x |
| y |
| О |
|
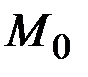
|
Р и с. 5.
Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная  , и большая, чем расстояние между фокусами
, и большая, чем расстояние между фокусами  (см. рис. 6).
(см. рис. 6).
b c2SgOq74IQ/w0LYu/v4ZCJmnOqOoclA4uVhG6oxSc7QTz2Oufld3LQ+gnv0HAAD//wMAUEsDBBQA BgAIAAAAIQCdb2Bi3AAAAAUBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI/BSgMxEIbvgu8QRvBmk5bS lHWzRQRF9KCtC17TzXQ3mEyWTdpdfXpTL3oZGP6fb74pN5N37IRDtIEUzGcCGFITjKVWQf3+cLMG FpMmo10gVPCFETbV5UWpCxNG2uJpl1qWIRQLraBLqS84j02HXsdZ6JFydgiD1ymvQ8vNoMcM944v hFhxry3lC53u8b7D5nN39AqWi4Nbvz2uXr6f6np8/lhaKV6tUtdX090tsIRT+ivDWT+rQ5Wd9uFI JjKnID+SfmfOpJBzYPszWErgVcn/21c/AAAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEB AAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9 If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAESm bfQWBgAAyCoAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAh AJ1vYGLcAAAABQEAAA8AAAAAAAAAAAAAAAAAcAgAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAE APMAAAB5CQAAAAA= ">
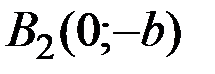
|
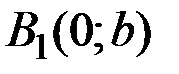
|
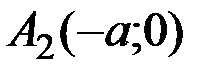
|

|
| у |
| х |
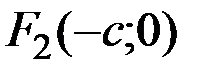
|
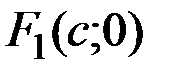
|
Р и с. 6.
Обозначим фокусы  и
и  , а расстояние между ними
, а расстояние между ними 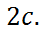
Расстояние 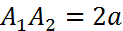 называется большей осью эллипса, а
называется большей осью эллипса, а  малой осью.
малой осью.
Каноническое уравнение эллипса с центром в начале координат имеет вид:
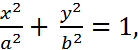 (13)
(13)
где 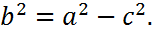 (14)
(14)
Определение. Отношение фокусного расстояния к длине большей оси называется эксцентриситетом эллипса и обозначается

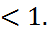 (15)
(15)
Определение. Гиперболой называется множество всех точек плоскости, разность расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 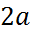 и меньшая, чем расстояние между фокусами
и меньшая, чем расстояние между фокусами  (см. рис. 7).
(см. рис. 7).
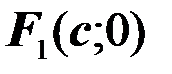
|

|
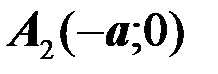
|
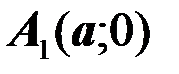
|
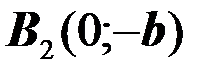
|

|
| o |
| x |
| y |
Р и с. 7.
Обозначим фокусы 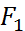 и
и  , а расстояние между ними.
, а расстояние между ними.
Расстояние 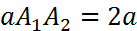 называется действительной осью гиперболы, а
называется действительной осью гиперболы, а 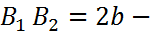 мнимой осью.
мнимой осью.
Прямые 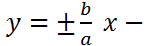 асимптоты гиперболы.
асимптоты гиперболы.
Каноническое уравнение гиперболы с центром в начале координат имеет вид:
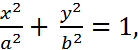 (16)
(16)
где 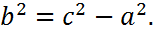 (17)
(17)
Определение. Отношение фокусного расстояния к длине действительной оси называется эксцентриситетом гиперболы и обозначается

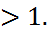 (18)
(18)
Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Определение. Расстояние от фокуса 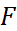 до директрисы называется параметром параболы и обозначается через
до директрисы называется параметром параболы и обозначается через 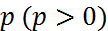 .
.
Канонические уравнения параболы с центром в начале координат:
1) Парабола симметрична относительно оси 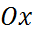 , фокус правее директрисы, ветви направлены вправо (см. рис 8).
, фокус правее директрисы, ветви направлены вправо (см. рис 8).
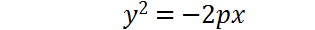 (19)
(19)
| y |
| x |
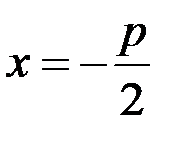
|
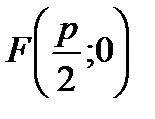
|
Р и с. 8.
2) Парабола симметрична относительно оси  фокус левее директрисы, ветви направлены влево (см.рис.9).
фокус левее директрисы, ветви направлены влево (см.рис.9).
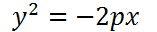 (20)
(20)
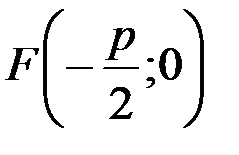
|
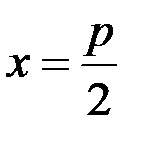
|
| y |
| x |
Р и с. 9.
3) Парабола симметрична относительно оси 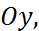 фокус выше директрисы, ветви направлены вверх (см.рис.10).
фокус выше директрисы, ветви направлены вверх (см.рис.10).

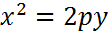 (21)
(21)
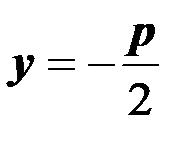
|
| y |
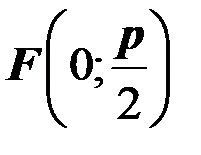
|
| x |
Р и с. 10.
4) Парабола симметрична относительно оси Oy, фокус ниже директрисы, ветви направлены вниз. (см.рис.11).
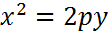 (22)
(22)
| y |
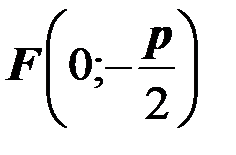
|
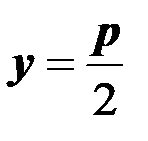
|
| x |
Р и с. 11.
Не нашли, что искали? Воспользуйтесь поиском: