
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения типовых заданий.
1. Даны вершины треугольника 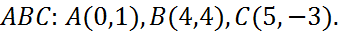 Найти:
Найти:
1.1 уравнение стороны  треугольника;
треугольника;
1.2 уравнение высоты 
1.3 уравнение медианы 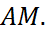
Решение. 1.1 Уравнение стороны 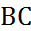 треугольника составим, воспользовавшись формулой (6):
треугольника составим, воспользовавшись формулой (6):
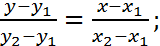

откуда  или
или 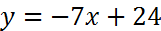 .
.
1.2 С учетом условия перпендикулярности двух прямых  и
и  , формула (10):
, формула (10): 
Тогда уравнение высоты  найдем по формуле (5):
найдем по формуле (5): 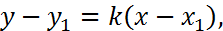 откуда
откуда 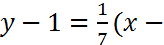
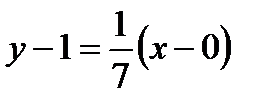 или
или 
1.3 Для того, чтобы найти координаты середины отрезка 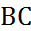 точки
точки  применим формулы (2):
применим формулы (2):
Имеем: 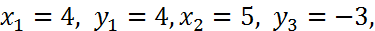 тогда
тогда
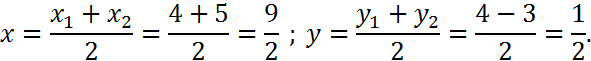
Уравнение медианы  составим по формуле (6):
составим по формуле (6): 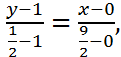
откуда  или
или 
2. Написать уравнение прямой, проходящей через точку 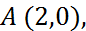 параллельно к прямой
параллельно к прямой 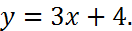
Решение. Так как прямая проходит через одну заданную точку, воспользуемся уравнением (5). Коэффициент  в нем найдем из условия параллельности прямых (9):
в нем найдем из условия параллельности прямых (9):

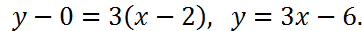
3. Найти расстояние от точки  до прямой
до прямой  если
если 
Решение. Предварительно составим уравнение прямой 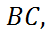 как прямой, проходящей через две заданные точки, формула (6):
как прямой, проходящей через две заданные точки, формула (6):

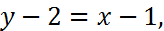
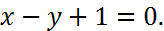
Расстояние от точки до прямой вычисляется по формуле (11):

4. Определить взаимное расположение двух прямых 
Решение. Находим: 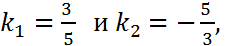 приведя оба уравнения к виду (4), видим, что
приведя оба уравнения к виду (4), видим, что 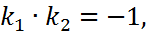 следовательно, прямые перпендикулярны.
следовательно, прямые перпендикулярны.
5. Найти угол между двумя прямыми 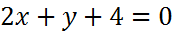
 .
.
Решение. Для того, чтобы определить угловые коэффициенты прямых I и II, приведем их уравнения к виду (4), выразив из обоих уравнений y:

Коэффициенты при  и есть угловые коэффициенты прямых
и есть угловые коэффициенты прямых
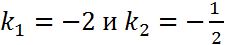 .
.
Угол между двумя прямыми находится по формуле (8):
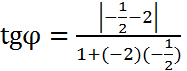 =
= 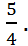
6. Определить вид кривой II порядка  используя метод выделения полных квадратов.
используя метод выделения полных квадратов.
Решение. Сгруппируем слагаемые, содержащие 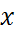 в одну скобку, а содержащие
в одну скобку, а содержащие  в другую:
в другую: 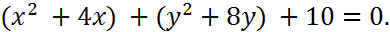 Дополним выражения в скобках до полных квадратов:
Дополним выражения в скобках до полных квадратов:

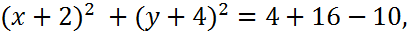
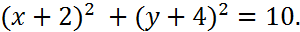
Получили уравнение окружности с центром в точке 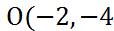 ) и радиусом
) и радиусом 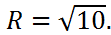
7. Написать уравнение окружности, диаметром которой служит отрезок 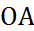 , где
, где 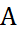
 ,а
,а  -начало координат.
-начало координат.
Решение. Для того, чтобы найти координаты центра кривой 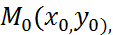 применим формулы (2) для нахождения координат середины отрезка:
применим формулы (2) для нахождения координат середины отрезка:
Имеем: 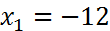 ,
,  тогда
тогда
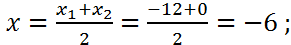

Радиус окружности найдем по формуле (1):
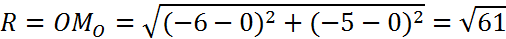
Воспользуемся нормальным уравнением окружности (12):
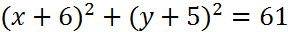 .
.
8. Составить каноническое yравнение эллипса, у которого большая полуось  а эксцентриситет
а эксцентриситет 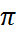 =
= 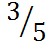 .
.
Решение. Каноническое уравнение эллипса имеет вид (13). Найдем малую полуось 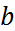 , используя формулу (14):
, используя формулу (14): 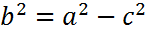 . Величину параметра
. Величину параметра 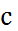 определим по формуле (13):
определим по формуле (13): 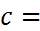
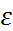 a=
a=  . Подставив значение с в формулу (14), получим:
. Подставив значение с в формулу (14), получим: 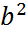 =
= 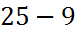 =16. Тогда, каноническое уравнение эллипса примет вид:
=16. Тогда, каноническое уравнение эллипса примет вид: 
9. Построить параболу, если задана ее директриса 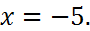
Решение: Каноническое уравнение параболы в данном случае имеет вид (19): 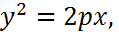 а уравнение ее директрисы
а уравнение ее директрисы  . Исходя из условия задания,
. Исходя из условия задания,  , отсюда
, отсюда 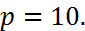 Каноническое уравнение кривой примет вид:
Каноническое уравнение кривой примет вид:  . Строим параболу:
. Строим параболу:
| y |
| x |
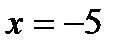
|
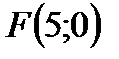
|
10. Вычислить эксцентриситет 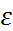 и определить фокусное расстояние
и определить фокусное расстояние  гиперболы
гиперболы 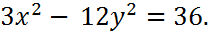
Решение. Приведем уравнение гиперболы к каноническому виду, разделив на 36 обе части равенства: 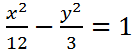 . Видим, что действительная полуось
. Видим, что действительная полуось  а мнимая полуось
а мнимая полуось  .
.
Для гиперболы справедливо равенство (17):  отсюда
отсюда 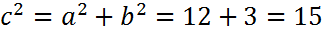 ,
, 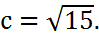 Тогда, фокусное расстояние
Тогда, фокусное расстояние  . Эксцентриситет гиперболы определим по формуле (18):
. Эксцентриситет гиперболы определим по формуле (18):  .
.
Список использованной литературы.
1. А. Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа: учебник для вузов. — Изд. 13-е, стереотип. — СПб. [и др.]: «Лань», 2006.
2. Г.Н. Берман. Сборник задач по курсу математического анализа. Решение типичных и трудных задач: учеб. пос. — Изд. 2-е, стереотип. — СПб.: «Лань», 2006.
3. Письменный Д.Т. Конспект лекций по высшей математике – М.: Айрис – пресс, 2002 – ч.1-2.
4. В.П. Минорский. Сборник задач по высшей математике. — М.: Физматлит, 2005.
5. Данко П.Е., Попов А.Г. Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Оникс, 2009
6. Индивидуальные задания по высшей математике. А.П. Рябушко (и др.); -3-е издание.- Минск: высшая школа, 2007. 1 часть -304 с.
7. Высшая математика для экономистов. Под редакцией Кремера Н.Ш. – 2-е изд.-М.: ЮНИТИ, 2002, 3-е изд.-М.: ЮНИТИ, 2010.
8. И.И. Привалов. Аналитическая геометрия: учебник. — Изд. 36-е, стер. — СПб. [и др.]: «Лань», 2007.
9. Д.В. Клетеник. Сборник задач по аналитической геометрии: уч. пособие для втузов. — 17-изд., стереотип. — СПб.: «Профессия», 2003.
Не нашли, что искали? Воспользуйтесь поиском: