
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Якщо в т. О відбувається коливання
Інтерференція
Розглянемо явище взаємного накладання двох хвиль, які одночасно існують у певній ділянці простору. Будемо вважати хвилі монохроматичними, тобто кожній з них відповідає гармонічне коливання з однією певною частотою:
 (4.18)
(4.18)
де j 01 і j 02 – початкові фази коливань джерел хвиль, r 1 і r 2 – відстані від джерел першої і другої хвилі до даної точки простору, w 1 і w 2 – циклічні частоти хвиль.
Різниця фаз двох хвиль у цій точці:
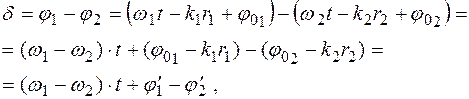 (4.19)
(4.19)
де j¢ 1 і j¢ 2 – початкові фази коливань у даній точці простору:
 (4.20)
(4.20)
Якщо зі зміною часу різниця фаз d у кожній точці простору зберігає своє значення, то при накладанні двох хвиль виникає явище їх взаємного підсилення або ослаблення, в залежності від величини d. Це явище отримало назву інтерференції.
Умова збереження у часі сталого значення різниці фаз двох хвиль для кожної точки простору називається когерентністю.
Дві хвилі називаються когерентними, якщо різниця їх фаз у кожній точці простору є сталою в часі.
Оскільки для фіксованої точки простору r 1 = const і r 2 = const, то
j¢ 1 – j¢ 2 = const.
Тоді різниця фаз двох хвиль у цій точці є сталою в часі лише за умови, що коефіцієнт при t в (4.19) дорівнює нулю, тобто w 1 = w 2.
Отже, когерентними можуть бути лише монохроматичні хвилі однакової частоти. За цієї умови d = j¢ 1 – j¢ 2 .
Щоб отримати дві когерентні світлові хвилі, застосовують метод поділу однієї хвилі на 2 частини, які потім накладаються одна на одну. При цьому утворюється інтерференційна картина, тобто чергування у просторі максимумів і мінімумів амплітуд коливань частинок, зумовлене інтерференцією двох хвиль.
Розглянемо це явище більш детально.
При взаємонакладенні двох когерентних хвиль у певній точці простору кожна частинка речовини, до якої дійшли ці хвилі, бере участь одночасно у двох коливаннях однакової частоти:
 (4.21)
(4.21)
Сумою цих двох коливань є також гармонічне коливання тієї ж самої частоти w, амплітуду якого можна визначити за допомогою методу векторних діаграм. В результаті знайдемо, що квадрат амплітуди результуючого коливання:
А 2 = А 12 + А 22 + 2 А 1 А 2 cos d, (4.22)
де d = j 1 – j 2 – різниця фаз двох хвиль у даній точці простору.
Інтенсивність світла І (середня густина потоку енергії електромагнітної хвилі) є пропорційною квадрату амплітуди світлової хвилі: I ~ A 2. Тому співвідношення (4.22) можна написати для інтенсивностей хвиль. Інтенсивність результуючого коливання в даній точці:
І = І 1 + І 2 + 2  cos d, (4.23)
cos d, (4.23)
де І 1 ~ А 12, І 2 ~ А 22 – інтенсивності коливань, що накладаються.
Таким чином, з останнього співвідношення маємо, що інтенсивність результуючого коливання залежить від різниці фаз d двох коливань, які накладаються в даній точці простору. При cos d =+ 1 утворюється максимум, при cos d = – 1 – мінімум. Якщо хвилі, що накладаються, мають однакові амплітуди: І 1 = І 2 =І 0, то в точках максимумів амплітуда результуючої хвилі зростає вчетверо: І max = 4 І 0, а в точках мінімумів – зменшується до нуля: І min = 0. Якщо І 1 ¹ І 2, інтерференційна картина має інше співвідношення максимумів і мінімумів.
З умови cos d =+ 1 знайдемо умову інтерференційного максимуму:
d max = ± 2 mp, (4.24)
а з умови cos d = – 1 – умову мінімуму:
d min = ±(2 m + 1) p, (4.25)
де m = 0, 1, 2,... – ціле число.
Різниця фаз d при інтерференції двох когерентних хвиль буде залежати від шляху, пройденого кожною з цих хвиль.
Нехай дві когерентні хвилі утворені в результаті поділу в точці О однієї хвилі на дві частини (Рис. 4.12). Їх інтерференцію будемо спостерігати у деякій точці М, до якої перша хвиля йде у середовищі з показником заломлення п 1, проходячи при цьому шлях l 1, а друга – в іншому середовищі з показником заломлення п 2, проходячи шлях l 2.

Згідно з (4.5), фазові швидкості хвиль:
 (4.26)
(4.26)
де с – швидкість світла у вакуумі.
Якщо в т. О відбувається коливання
 ,
,
то в т. М перша хвиля збуджує коливання:
 , (4.27)
, (4.27)
а друга:  . (4.28)
. (4.28)
Різниця фаз хвиль, враховуючи (4.26):
 , (4.29)
, (4.29)
або: 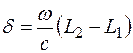 , (4.30)
, (4.30)
де L = l× n – оптична довжина ходу світлової хвилі.
Введемо позначення: D = L 2 – L 1 – оптична різниця ходу двох хвиль.
Враховуючи співвідношення (3.225), знайдемо w/с =2p/l = k – хвильове число, що відповідає розповсюдженню хвилі даної частоти у вакуумі (l – довжина хвилі у вакуумі). Тоді (4.30) набере вигляду:
 . (4.31)
. (4.31)
Це співвідношення дає змогу визначити умови інтерференційних максимумів і мінімумів не для різниці фаз, а для оптичної різниці ходу когерентних хвиль, що накладаються при інтерференції. Підставляючи (4.24) і (4.25) в (4.31), отримаємо:
умова максимуму: D max = ± ml, (4.32)
умова мінімуму:
D min = ±(2 m + 1) l/2. (4.33)
Отже, у просторі спостерігається чергування інтерференційних максимумів і мінімумів, які разом утворюють інтерференційну картину.
Інтерференційні максимуми утворюються в тих точках, де оптична різниця ходу хвиль дорівнює парному числу півхвиль (враховуючи, що ml = 2 m (l/ 2)), мінімуми – де оптична різниця ходу дорівнює непарному числу півхвиль.
Не нашли, что искали? Воспользуйтесь поиском: