Дифракція Фраунгофера на щілині

На відміну від дифракції Френеля, при дифракції Фраунгофера джерело світла і точка спостереження знаходяться на нескінченних відстанях від перешкоди, що викликала дифракцію. Це означає, що хвильові поверхні є плоскими, а окремі промені світла є взаємно паралельними всередині світлового пучка. На практиці цей випадок можна реалізувати за допомогою лінз. Якщо помістити джерело світла у фокус лінзи, отримаємо після лінзи паралельний світловий пучок. А перенести точку спостереження з нескінченності в певну точку простору можна, якщо сфокусувати в цю точку паралельний пучок світла за допомогою іншої лінзи.

Розглянемо дифракцію Фраунгофера на нескінченно довгій щілині. Нехай плоска монохроматична хвиля падає перпендикулярно на непрозорий екран зі щілиною шириною а (Рис. 4.22). За екраном розглянемо хвилю, що розповсюджується в довільному напрямку під кутом j відносно нормалі до екрану. Ця хвиля генерується вторинними джерелами у площині щілини, і її амплітуда залежить від числа зон Френеля у щілині.

Границі зон Френеля визначаються за тим же принципом: оптична різниця ходу світла від країв однієї зони дорівнює l/ 2.

Ширина однієї зони:

. (4.51)

Таким чином, всього на ширині щілини поміщується кількість зон Френеля:

N = . (4.52)

Різниця ходу від сусідніх зон дорівнює l /2, тобто вони створюють коливання, які є протифазними. Оскільки ширина всіх зон однакова, то амплітуди коливань, створених кожною зоною, також однакові. Тому при складанні коливань двох сусідніх зон вони взаємно компенсуються, даючи в результаті нуль. Таким чином, при розрахунку амплітуди коливань в даному напрямку (під кутом j) можна виключити з розрахунку всі пари сусідніх зон Френеля, оскільки вони не будуть давати внесок в кінцевий результат. Амплітуда результуючого коливання буде визначатись не більше, ніж однією некомпенсованою зоною, або частиною зони.

Якщо на ширині щілини вкладається точно парне число зон Френеля (N = 2 m), то вони взаємно компенсують одна одну, і в даному напрямку спостерігається дифракційний мінімум (амплітуда коливань дорівнює нулю). Порівнюючи з (4.52), маємо умову мінімуму:

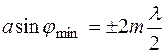, (4.53)

де т = 1,2,3,… – ціле число.

Дифракційний максимум утворюється при умові, що некомпенсованою залишається ціла зона Френеля, а не її частина, тобто на ширині щілини точно вкладається непарне число зон Френеля (N = 2 m + 1):

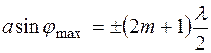. (4.54)

Отже, в залежності від кута j маємо чергування світлих і темних смуг. При цьому в прямому напрямку (j = 0) щілина діє як одна зона Френеля, і в цьому напрямку спостерігається найбільш інтенсивний центральний дифракційний максимум. В цілому, розподіл інтенсивності світла в залежності від кута j зображено в нижній частині рис. 4.22.

Дифракційна гратка

Як видно з умови (4.54), напрямок кожного дифракційного максимуму при дифракції на щілині залежить від довжини хвилі світла. Тому при взаємодії немонохроматичного світла (наприклад, білого), яке має в своєму складі хвилі з різними довжинами l, воно розкладається в спектр, у якому кожній довжині хвилі відповідає свій напрямок. Після розкладання в спектр білого світла і його проектування на екран на місці кожного дифракційного максимуму (крім центрального) утворюється різнокольорова смужка на зразок райдуги.

Проте, дифракція на одній щілині дає надто широкі і надто слабкі бічні максимуми, а тому розкладання світла в спектр за її допомогою є малоефективним. Значно кращий результат можна отримати за допомогою дифракційної гратки (інша назва – дифракційна решітка).

Дифракційна гратка – це система паралельних щілин рівної ширини, розміщених через рівні проміжки.

На рис. 4.23а схематично зображена типова дифракційна гратка – скляна пластинка з нанесеним на неї за допомогою спеціального обладнання рядом паралельних непрозорих штрихів через рівні проміжки. На рис. 4.23б показаний фрагмент дифракційної гратки у збільшеному вигляді. Якщо ширину щілин позначити через а, а ширину непрозорих проміжків – через b, то періодом гратки називається величина d = a + b. На практиці досить часто як головний параметр дифракційної гратки називають n = N/L – число штрихів на одиницю довжини. Період гратки є величиною, оберненою до цього параметру: d = 1 /n.

У дифракційній гратці на кожній щілині відбувається дифракція Фраунгофера аналогічно тому, як і у випадку окремої щілини, тобто виникають максимуми і мінімуми, напрямки яких визначаються співвідношеннями (4.53) і (4.54). Але на них накладаються ще й додаткові мінімуми, зумовлені взаємною інтерференцією променів від різних щілин, за рахунок якої у певних напрямках вони взаємно погашають один одного.

Умова додаткових мінімумів:

, (4.55)

де N – число щілин; k = 1, 2,... N – 1, N +1,... – ціле число, яке може набувати будь-яких цілочисельних значень, крім 0, N, 2 N,..., тобто тих, при яких коефіцієнт перед l в (4.55) дорівнює цілому числу.

Якщо коефіцієнт перед l в (4.55) дорівнює цілому числу т, то у відповідних напрямках виникає взаємне підсилення променів за рахунок інтерференції променів від різних щілин (різниця ходу променів від сусідніх щілин дорівнює цілому числу хвиль). У цих напрямках спостерігаються так звані головні максимуми, умовою яких є:

d sin j _max = ± ml. (4.56)

Таким чином, із наведених співвідношень можна зробити висновок, що в цілому розподіл по кутах j інтенсивності світла після його проходження через дифракційну гратку має вигляд вузьких інтенсивних головних максимумів, між якими знаходяться (N – 1) додаткових мінімумів, розділених слабкими вторинними максимумами. Зі збільшенням кількості щілин зростає інтенсивність і контраст головних максимумів. На Рис.4.24 наведено приклад такого розподілу для дифракційної гратки, в якій загальна кількість щілин N = 6.

Загальну кількість головних максимумів можна визначити з (4.56), враховуючи умову , звідки

. (4.57)

Кутова орієнтація головних максимумів, згідно з (4.56), залежить від довжини хвилі l, тому при проходженні через гратку білого світла всі максимуми, крім центрального (m = 0), розкладуться у спектр. Цей розклад у спектр є набагато більш якісним, порівняно з дифракцією на одній щілині, оскільки головні максимуми є дуже вузькими, а тому майже не відбувається взаємонакладення різних кольорів один на одного. Для того, щоб можна було отримати щонайменше один бічний максимум, необхідно виконати умову (див. (4.57)) d > l.

В залежності від періоду гратки d, вона може працювати в певному діапазоні довжин хвиль. Створені гратки з періодом в долі мікрометра, за допомогою яких можна досліджувати спектри не лише у видимому, але і в ультрафіолетовому діапазонах. Для дослідження більш короткохвильового випромінювання (жорстке ультрафіолетове та рентгенівське) застосовуються атомні періодичні структури типу дифракційних ґраток на основі кристалів.

Не нашли, что искали? Воспользуйтесь поиском: