Методи спостереження інтерференції

Абсолютно монохроматичних хвиль у природі не існує. Але можна створити умови, за яких джерело світла випромінює електромагнітні хвилі у дуже вузькому діапазоні частот. При цьому з деяким наближенням можна вважати, що світло є монохроматичним. Світло, близьке до монохроматичного, випромінюють атоми при переходах електронів між певними енергетичними рівнями. Саме таку природу має випромінювання квантових генераторів (лазерів). Лазери є найбільш досконалими з усіх існуючих на даний час джерел монохроматичного світла. Інший спосіб отримання світла, близького до монохроматичного, – виділення із загального світлового потоку, який складається з випромінювання різних частот, одного вузького частотного діапазону за допомогою фільтрів.

Для отримання інтерференційної картини необхідно здійснити взаємонакладення двох когерентних хвиль. Для цього застосовують метод поділу монохроматичної хвилі на 2 частини, які потім накладаються одна на одну.

Історично першими методами, які були застосовані для спостереження інтерференції, були методи Юнга і Френеля. Крім того, на практиці досить часто використовується інтерференція світла в тонких плівках.

Метод Юнга

У цьому методі джерелами когерентних хвиль S ₁ і S ₂ є дві вузькі паралельні щілини, прорізані у непрозорому екрані Е ₁, який освітлюється монохроматичним світлом від джерела S (Рис. 4.14). Таким чином здійснюється поділ одного світлового потоку на два, що взаємонакладаються у просторі за екраном Е ₁ і утворюють інтерференційну картину, яка може спостерігатися на екрані Е ₂. Згідно зі співвідношенням (4.39), для утворення досить широких і зручних для вимірювань інтерференційних смуг необхідно по можливості збільшувати відстань між екранами Е ₁ і Е ₂, а також зменшувати відстань між щілинами S ₁ і S ₂. Для забезпечення когерентності джерел S ₁ і S ₂ ширина щілин повинна бути досить малою порівняно з відстанню між ними. Оскільки освітленість екрану Е ₂ є пропорційною ширині щілин, то інтенсивність інтерференційної картини у методі Юнга є дуже низькою.

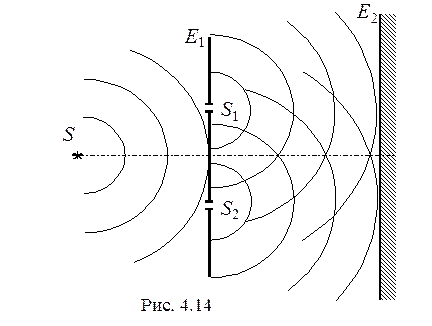
Метод Френеля

Інтерференційна картина у методі Юнга має дуже слабку інтенсивність, і її важко спостерігати навіть у затемненому приміщенні. Цей недолік усунений у методі Френеля. В цьому методі поділ на дві частини світлового потоку від монохроматичного джерела S відбувається при його відбиванні від двох плоских дзеркал Д ₁ і Д ₂, площини яких розміщені під невеликим кутом a одна відносно одної (Рис. 4.15). Завдяки цьому два зображення джерела S у дзеркалах (уявні джерела S ₁ і S ₂) розміщені на невеликій відстані d. Відбиті від дзеркал світлові пучки є взаємно когерентними, оскільки це дві частини світлового потоку від одного джерела S.

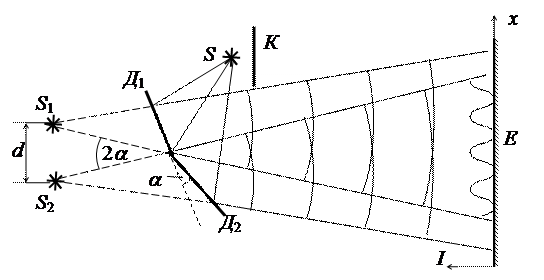Рис. 4.15

Інтерференційна картина у вигляді паралельних світлих і темних смуг спостерігається на екрані Е в зоні перекриття двох світлових пучків від дзеркал Д ₁ і Д ₂. Для запобігання падіння на екран прямих променів світла від джерела S встановлений непрозорий екран К. Інтенсивність інтерференційної картини є пропорційною ширині ділянок дзеркал, які створюють освітленість у зоні перекриття, і значно перевищує інтенсивність картини при застосуванні методу Юнга.

Інтерференція в тонких плівках

У методах Юнга і Френеля для утворення інтерференційної картини використовуються дві частини світлового пучка, які від первинного джерела S розповсюджуються по різних траєкторіях. Але можливим є й інший спосіб поділу світлового пучка на дві частини, у якому кожний промінь при падінні на границю розділу двох середовищ утворює два променя: відбитий та заломлений (див. рис. 4.1). Ці промені є взаємно когерентними, і при їх взаємонакладенні утворюється інтерференційна картина. Це явище можна спостерігати при відбиванні світла від тонких прозорих плівок.

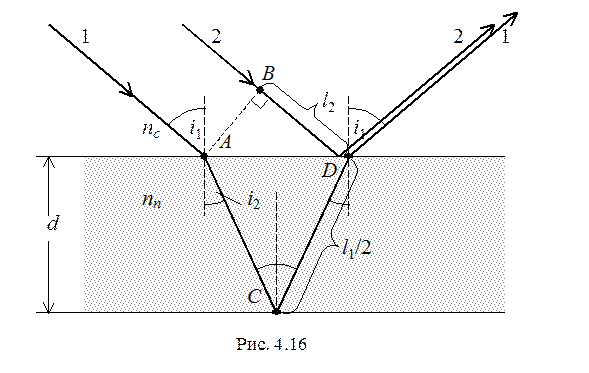Розглянемо прозору плоскопаралельну пластинку товщиною d, на яку з певного середовища падає паралельний пучок світла з довжиною хвилі l під кутом і ₁ відносно нормалі (Рис. 4.16). Частина світла в результаті заломлення пройде всередину пластинки, відіб’ється від нижньої границі і, заломившись ще раз на верхній границі, знову вийде назовні (промінь 1), а друга частина відіб’ється від верхньої границі пластинки (промінь 2). Неважко переконатися, що промені 1 і 2 після відбивання йдуть у зовнішньому середовищі паралельно. При їх взаємонакладенні буде спостерігатись інтерференція, оскільки вони є когерентними (це дві частини випромінювання від одного джерела). Промені, утворені в результаті багаторазових відбивань від границь пластинки, враховувати не будемо внаслідок їх малої інтенсивності.

Для досить поширеного випадку, коли тонка плівка з показником заломлення n_п знаходиться в повітрі (п_с» 1), величину оптичної різниці ходу можна розрахувати, застосовуючи закони відбивання та заломлення світла, а також тригонометричні співвідношення. В результаті отримаємо:

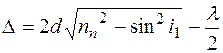, (4.42)

де l – довжина хвилі світла у вакуумі.

З (4.42) можна зробити висновок, що для даної тонкої плівки є дві можливості змінити різницю ходу хвиль:

1) зміна товщини плівки d;

2) зміна кута падіння променів і ₁.

Таким чином, якщо кут падіння променів є сталим у всіх точках поверхні плівки (і ₁= const), то при спостереженні інтерференції максимуми і мінімуми мають вигляд смуг (світлих і темних), які проходять вздовж плівки. При цьому виконання умов інтерференції забезпечується тим, що вздовж кожної окремо взятої смуги товщина плівки залишається сталою (d = const). Інтерференційні смуги такого типу називаються смугами рівної товщини. За картиною смуг рівної товщини можна зробити висновок про характер рельєфу тонкої плівки з великою точністю – до долів довжини хвилі видимого світла (десяті і соті долі мікрометра). Класичним прикладом інтерференційних смуг рівної товщини є так звані кільця Ньютона.

Якщо, навпаки, сталою є товщина плівки (d = const), то умови максимумів і мінімумів, згідно з (4.42), виконуються для певних кутів падіння променів і ₁. Відповідні інтерференційні смуги (смуги рівного нахилу), кожна з яких відповідає певному куту падіння, можна спостерігати, якщо спроектувати інтерференційну картину на екран за допомогою лінзи.

Інтерференція в тонких плівках досить часто спостерігається у повсякденному житті. Наприклад, саме цим явищем пояснюється виникнення різнобарвних плям і смуг на поверхні води, забрудненої нафтопродуктами, які утворюють надзвичайно тонку прозору плівку. Інший приклад – поява кольорового блиску на поверхні металу після його нагрівання до високої температури. В цьому випадку прозора плівка утворюється внаслідок появи окалини (тонкий шар оксиду металу). Різнокольорові переливи таких плівок пояснюються тим, що у білому світлі умови інтерференційних максимумів у різних місцях плівки реалізуються для світла різної частоти (різного кольору). Неодмінною умовою такої інтерференції є досить мала товщина плівки, сумірна з довжиною хвилі світла.

Це явище має також багато корисних застосувань:

- виготовлення “просвітлених” оптичних приладів (лінз, призм) з низьким коефіцієнтом відбивання світла;

- виготовлення селективних дзеркал з коефіцієнтом відбивання світла, близьким до 1, у вузькому спектральному діапазоні;

- контроль рельєфу плоскої поверхні на мікроскопічному рівні.

Не нашли, что искали? Воспользуйтесь поиском: