Теоретичні відомості про скалярний, векторний та мішаний добутки

1. Відстань між точками обчислюється за формулою: .

2. Скалярним добутком векторів і називається число, яке дорівнює добутку модулів цих векторів на косинус кута між ними:

3. Два ненульові вектори перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.

4. Кут між векторами визначають за формулою:

5. Якщо вектори задано за допомогою координат: 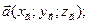, то скалярний добуток обчислюється так:

.

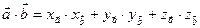6. Векторним добутком векторів і називається вектор , який задовольняє такі умови:

· ;

· ;

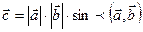· Трійка векторів ; і - права.

7. Два вектори колінеарні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.

8. Модуль векторного добутку чисельно дорівнює площі паралелограма, побудованого на векторах і як на сторонах.

9. Площа трикутника, побудованого на векторах і як на сторонах обчислюється за формулою:

10. Якщо 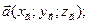, то векторний добуток векторів має вигляд:

=

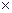
11. Мішаним добутком трьох векторів ; і називають число, яке дорівнює векторному добутку двох перших векторів, помноженому скалярно на третій. Тобто:

=

12. Три вектори будуть компланарними тоді і тільки тоді, коли їх мішаний добуток дорівнює нулю.

13. Модуль мішаного добутку чисельно дорівнює об’єму паралелепіпеда, побудованого на цих векторах як на ребрах.

14. Об’єм трикутної піраміди, побудованої на векторах ; і як на ребрах знаходять за формулою:

.

15. Якщ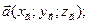о ; , то = .

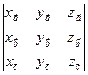Задача. Дано вершини трикутної піраміди А(1, -3, 2), В(-1, 1, 6), С(-9, 8, 4), D(2, -1, 2). Знайти:

1. Координати та довжину вектора ;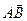

2. Внутрішній кут 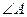трикутника ;

3. Площу грані ;

4. Об’єм піраміди .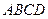

Питання длясамоперевірки знань, вмінь

1. Що називається скалярним добутком векторів?

2. Умова перпендикулярності двох ненульових векторів.

3. Формула кута між двома векторами.

4. Що називається векторним добутком векторів?

5. Умова колінеарності векторів.

6. Чому дорівнює модуль векторного добутку векторів?

7. Як обчислити площу трикутника, побудованого на двох векторах як на сторонах?

8. Що називається мішаним добутком трьох векторів?

9. Умова компланарності трьох векторів.

10. Чому дорівнює модуль мішаного добутку?

11. Як обчислити об’єм піраміди побудованої на трьох векторах як на ребрах?

Висновок______________________________________________________________________________________________________________________________________________________________________________________________

Перевірив викладач ___________ Оцінка___________Дата ______________

Не нашли, что искали? Воспользуйтесь поиском: