Теоретичні відомості про диференціал функції.

Головну, лінійно залежну від Δх, частину приросту Δy функції y=f(x), тобто величину 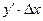, називають диференціалом функції і назначають dy або d(f(x)). Отже, .

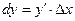Диференціал аргументу дорівнює його приросту dх= Δх. Тому .

Отже, щоб знайти диференціал функції y=f(x), слід знайти похідну 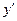цієї функції і помножити цю похідну на диференціал аргументу dx.

Диференціал використовують для наближених обчислень:

1. Для дуже малих значень Δх 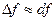, тобто .

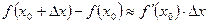2. Для знаходження наближених значень функцій використовують формулу:

.

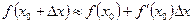Задача № 1. Обчислити диференціал функції 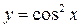при x =π/4 і dx=0,03.

Задача № 2. Знайти наближене значення приросту функції 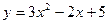в точці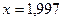

Задача № 3.

а) Обчислити наближене значення функції 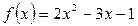при x =2,01

б) Знайти наближене значення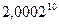

Питання для самоконтролю знань, умінь

1. Похідна суми, добутку, частки двох функцій.

2. Похідна складеної функції.

1. Похідна степеневої функції.
2. Похідні логарифмічної, показникової та тригонометричних функцій.
3. Що називається диференціалом?
4. Геометричний зміст диференціала
5. Як за допомогою диференціала можна знайти наближене значення приросту функції?
6. Як обчислити наближене значення функції за допомогою диференціала?

Висновок__________________________________________________________________________________________________________________________________________________________________________________

Перевірив викладач ___________ Оцінка ___________ Дата___________

Не нашли, что искали? Воспользуйтесь поиском: