Теоретичні відомості про екстремум функції

Теорема (друге правило). Якщо в точці похідна 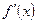функції дорівнює нулю, а її друга похідна неперервна в околі цієї точки і 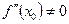, то функція має максимум в точці , коли і мінімум, коли .

Задача №2. Знайти максимум і мінімум функції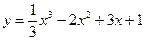

Задача №3. Знайти довжини сторін прямокутника з периметром 72 см, що має найбільшу площу.

Теоретичні відомості про застосування похідної

1. Фізичний зміст похідної. При прямолінійному русі точки швидкість в даний момент дорівнює похідній від шляху по часу , обчисленій при : .

Прискорення в даний момент дорівнює похідній від швидкості по часу , обчисленій при : .

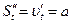2. Геометричний зміст похідної. Похідна 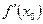дорівнює кутовому коефіцієнту дотичної до кривої, проведеної у точці 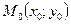. Рівняння дотичної до графіка функції в точці з абсцисою має вигляд: .

Задача №4. Знайти швидкість і прискорення точки, що рухається за законом 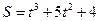в момент часу .

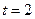Задача №5. Скласти рівняння дотичної до графіка функції в точці з абсцисою .

Питання для самоконтролю знань, умінь

1. Які точки називаються критичними?

2. Правило знаходження найбільшого та найменшого значення функції.

3. Які точки називаються точками максимуму і точками мінімуму?

4. Перше правило відшукання екстремуму функції.

5. Друге правило відшукання екстремуму функції.

6. Фізичний зміст похідної.

7. Геометричний зміст похідної. Рівняння дотичної до графіка функції.

Висновок __________________________________________________________________

____________________________________________________________________________________________________________________________________

Перевірив викладач_________________ Оцінка _________Дата________

Не нашли, что искали? Воспользуйтесь поиском: