
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение задач с пропорциональными величинами.
Решение задач с пропорциональными величинами вызывает значительные трудности у младших школьников. Одна из причин заключается в том, что понятие «пропорциональная зависимость» не является предметом специального изучения и усвоения. Именно поэтому методика работы над такими задачами должна обеспечивать наиболее полную реализацию их обучающего потенциала.
Связи между пропорциональными величинами раскрываются с помощью решения простых задач на нахождение одной из величин по данным, соответствующим значениям двух других величин (например, задача на нахождение стоимости по известным цене и количеству). Поэтому при решении простых задач с пропорциональными величинами (а затем и составных) целесообразно использовать методические приемы, способствующие формированию у учащихся представлений о пропорциональной зависимости величин. К таким приемам относятся: интерпретация текста задачи с помощью таблицы и чертежа; сравнение результатов решения задач, в которых изменяется одно из данных; составление и решение обратных задач; выбор решения задачи; анализ текстов задач с недостающими и лишними данными.
Уточним для себя понятия «величина» и «пропорциональная зависимость».
Представьте себе, что вы едете в поезде. Время от времени вы смотрите на часы и замечаете, как долго вы уже находитесь в пути. Вы говорите, например, что со времени отправления вашего поезда прошло 2, 3, 5, 10, 15 часов и т. д. Эти числа обозначают различные промежутки времени; они называются значениями этой величины (времени). Или вы смотрите в окно и следите по дорожным столбам за расстоянием, которое проходит ваш поезд. Перед вами мелькают числа 110, 111, 112, 113, 114 км. Эти числа обозначают различные расстояния, которые прошёл поезд от места отправления. Они тоже называются значениями, на этот раз другой величины (пути или расстояния между двумя пунктами). Таким образом, одна величина, например, время, расстояние, температура, может принимать сколько угодно различных значений.
Обратите внимание на то, что человек почти никогда не рассматривает только одну величину, а всегда связывает её с какими-нибудь другими величинами. Ему приходится одновременно иметь дело с двумя, тремя и большим числом величин. Представьте себе, что вам нужно к 9 часам попасть в школу. Вы смотрите на часы и видите, что в вашем распоряжении 20 минут. Тогда вы быстро соображаете, стоит ли вам садиться в трамвай или вы успеете дойти до школы пешком. Подумав, вы решаете идти пешком. Заметьте, что в то время, когда вы думали, вы решали некоторую задачу. Эта задача стала простой и привычной, так как вы решаете такие задачи каждый день. В ней вы быстро сопоставили несколько величин. Именно вы посмотрели на часы, значит, учли время, затем вы мысленно представили себе расстояние от вашего дома до школы; наконец, вы сравнили две величины: скорость вашего шага и скорость трамвая, и сделали вывод, что за данное время (20 мин.) вы успеете дойти пешком. Из этого простого примера вы видите, что в нашей практике некоторые величины связаны между собой, т. е. зависят друг от друга.
Рассмотрим задачу, в условие которой входят две величины: расстояние и время. Задача 1. Тело, движущееся прямолинейно и равномерно, проходит в каждую секунду 12 см. Определить путь, пройденный телом в 3, 5,..., 10 секунд.
Составим таблицу, по которой можно было бы следить за изменением времени и расстояния.

Таблица даёт нам возможность сопоставить эти два ряда значений. Мы видим из неё, что когда значения первой величины (времени) постепенно увеличиваются в 3, 5,..., 10 раз, то и значения второй величины (расстояния) тоже увеличиваются в 3,5,..., 10 раз. Таким образом, при увеличении значений одной величины в несколько раз значения другой величины увеличиваются во столько же раз, а при уменьшении значений одной величины в несколько раз значения другой величины уменьшаются во столько же раз.
Рассмотрим теперь задачу, в которую входят две такие величины: количество материи и ее стоимость.
Задача 2. 15 м ткани стоят 120 руб. Вычислить стоимость этой ткани для нескольких других количеств метров, указанных в таблице.
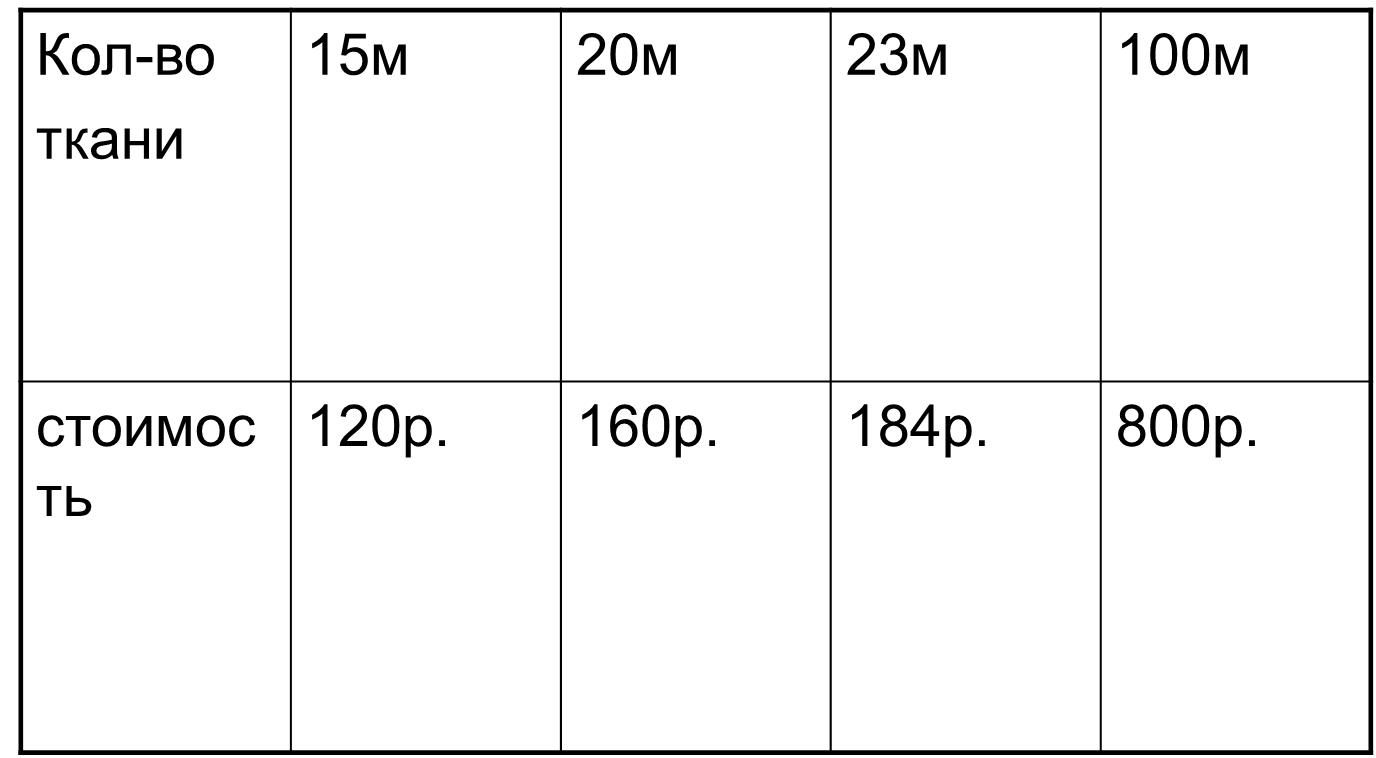
По этой таблице мы можем проследить, каким образом постепенно возрастает стоимость товара в зависимости от увеличения его количества. Несмотря на то что в этой задаче фигурируют совсем другие величины (в первой задаче -- время и расстояние, а здесь -- количество товара и его стоимость), тем не менее в поведении этих величин можно обнаружить большое сходство.
Пары величин, с которыми мы встретились в первой и второй задачах, называются прямо пропорциональными. Таким образом, если две величины связаны между собой так, что с увеличением (уменьшением) значения одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз, то такие величины называются прямо пропорциональными. О таких величинах говорят также, что они связаны между собой прямо пропорциональной зависимостью. В природе и в окружающей нас жизни встречается множество подобных величин. Приведём примеры:
1. Время работы (день, два дня, три дня и т. д.) и заработок, полученный за это время при подённой оплате труда.
2. Объём какого-нибудь предмета, сделанного из однородного материала, и вес этого предмета.
Рассмотрим следующую задачу: «Пять каменщиков могут сложить кирпичные стены дома в 168 дней. Определить, во сколько дней могли бы выполнить ту же работу 10, 8, 6 и т. д. каменщиков».
Если 5 каменщиков сложили стены дома за 168 дней, то (при одинаковой производительности труда) 10 каменщиков могли бы выполнить это вдвое скорее, так как в среднем 10 человек выполняют работу в два раза большую, чем 5 человек.
Составим таблицу, по которой можно было бы следить за изменением числа рабочих и рабочего времени.
| Кол-во рабочих | 10чел. | 8чел. | 6чел. | 5чел. |
| Время работы | 84д. | 105д. | 140д. | 168д. |
Например, чтобы узнать, сколько дней потребуется 6 рабочим, надо сначала вычислить, сколько дней требуется одному рабочему (168* 5 =840), а затем - шести рабочим (840: 6 = 140). Рассматривая эту таблицу, мы видим, что обе величины приняли различные значения. Каждому значению первой величины соответствует определённое; значение второй величины, например, 10- соответствует 84, числу 8 -- число 105 и т. д.
Если мы будем рассматривать значения обеих величин слева направо, то увидим, что значения верхней величины убывают, a значения нижней возрастают. Возрастание и убывание подчинено следующему закону: значения числа рабочих увеличиваются во столько же раз, во сколько раз уменьшаются значения затраченного рабочего времени. Ещё проще эту мысль можно выразить так: чем больше занято в каком-либо деле рабочих, тем меньше им нужно времени для выполнения определённой работы. Две величины, с которыми мы встретились в этой задаче, называются обратно пропорциональными.
В жизни встречается много подобных величин. Приведём примеры. Если на 150 руб. нужно купить несколько килограммов конфет, то количество конфет будет зависеть от цены одного килограмма. Чем выше цена, тем меньше можно купить на эти деньги товара. С повышением в несколько раз цены конфет уменьшается во столько же раз число килограммов конфет, какое можно купить на 150 руб. В этом случае две величины (вес товара и его цена) обратно пропорциональны.
Приведем примеры заданий на пропорциональные величины, встречающиеся в учебниках начальной школы.
· Постройте чертеж и решите задачу: «В 3 ведрах 30 л молока. Сколько молока в 9 таких же ведрах?»
· Решите задачу двумя способами: «В 6 одинаковых домах 24 подъезда. Сколько подъездов в 12 таких же домах?»
· Составьте схему решения задачи: «В 4 тетрадях 48 листов. Сколько листов в 7 таких же тетрадях?»
· Выберите выражение, которое является решением задачи: «Бабушка связала 4 одинаковые шапочки из 12 мотков шерсти. Сколько мотков шерсти понадобиться на 8 таких шапочек?»
а) 12: 4 • 8 = 24(м.)
б) 12: 4 - 8 = 5(м.)
в) 12 • (8: 4) = 24(м.)
г) 12: (8 - 4) = 3(м.)
· Постройте таблицу и решите задачу: «На пошив 8 одинаковых пальто израсходовали 24 м ткани. Сколько ткани потребуется на 2 таких же пальто?»
В начальной школе рассматривают различные процессы и величины, характеризующие их. (см. таблицу)
| Процессы | Величины, характеризующие процесс |
| Равномерное движение | Скорость, время, расстояние (пройденный путь) |
| Купля - продажа | Цена, количество, стоимость |
| Измерение массы | Масса одного предмета, число предметов, масса всех предметов |
| Нахождение площади прямоугольника | Длина, ширина, площадь прямоугольника |
| Расходование материалов | Норма расходования материала на одно изделие, число изделий, расход материалов на все изделия |
| Работа | Производительность труда, время работы, весь объем работы |
| Сбор урожая | Урожайность, площадь посева, весь урожай, собранный с этой площади. |
Процесс формирования у младших школьников умения решать задачи на пропорциональную зависимость предполагает несколько этапов.
I этап ориентирован на обучение учащихся выделять тройку величин из текста.
Предварительно необходимо провести подготовительную работу. Для начала предложим ученикам несколько групп величин.
| Мерка | Количество мерок | Целое |
| Расход материи на одну вещь | Число вещей | Весь расход материи |
| Масса одного предмета | Число предметов | Вся масса |
| Сахара на один стакан варенья | Число стаканов | Всего сахара |
| Блинов на одной порции | Число порций | Всего блинов |
| Стёкол на одно окно | Число окон | Всего стёкол |
| Листов бумаги в одном наборе | Число наборов | Всего листов |
| Человек сидит за одним столом | Число столов | Всего человек |
| Расход материи на одну вещь | Число вещей | Весь расход материи |
Данную таблицу целесообразно проанализировать. Для этого надо предложить детям следующие вопросы:
– Что общего в первом столбце?
- Во втором столбце?
- В третьем столбце?
– Что разъясняет мерка? Количество мерок? Целое?
– Каков порядок записи величин в таблице?
Затем надо предложить ученикам сопоставить эту таблицу со следующей.
Дети должны определить: Что изменилось в первом столбце
второй таблицы? Что можно сказать о числе объектов в каждой группе предметов?
| Мерка | Количество мерок | Целое |
| Книг в каждой посылке | Число посылок | Всего книг |
| Игрушек, изготовленных каждой группой | Число групп | Всего игрушек |
| Открыток в каждой пачке | Число пачек | Всего открыток |
| Человек в каждой команде | Число команд | Всего человек |
На этом этапе наиболее сложным для учащихся является выделение мерки. Кроме анализа таблиц можно предложить составить по ним тексты задач, дополняя их числовыми данными и их схематические модели. Так же можно предложить задания на заполнение таблицы - дополнение неизвестных величин и подведение каждого столбика величин под понятие.
| ? | ? | ? |
| Предметов в одной коробке | ? | Всего предметов |
| ? | Число пачек | Всего учебников |
| Деревьев в каждом ряду | ? | Всего деревьев |
| ? | ? | ? |
После того, как ученики поняли принцип построения тройки величин, предлагаем выделить их в задаче.
При анализе задач, предлагаем выделить тройку величин: мерка, количество мерок, целое и записать это в таблице.
| Мерка | Количество мерок | Целое |
Например:
ü В классе 8 двухместных парт. Сколько всего мест в классе?
ü В классе 8 одноместных парт. Сколько всего мест в классе?
ü Сколько обезьян сидит в клетке, если всего у них 36 ног?
ü Сколько куриц сидит в клетке, если всего у них 36 ног?
Чтобы помочь ученикам определить мерку стоит использовать наглядный материал.
II этап направлен на приобретение учащимися умения раскрывать связи между величинами. Важным инструментом для решения этой задачи является построение вспомогательной модели задачи. Её можно представить в виде таблицы или схемы:
целое
мерка…………………..мерка
количество мерок
| Мерка | Количество мерок | Целое |
Если ребёнок знает правила нахождения величины на языке схемы, то при определенной системе упражнений он сможет их переформулировать на естественный язык:
III этап предполагает обучение умению решать простые текстовые задачи.
Умение включает в себя:
– выделение тройки величин из текста;
– табличное или схематическое моделирование задачи (в зависимости от учебной программы либо умений детей);
– осуществление поиска способа решения задачи на основе нахождения неизвестной величины по двум известным, используя алгоритмы:
ü Чтобы найти мерку, нужно целое разделить на количество мерок.
ü Чтобы найти количество мерок, нужно целое разделить на мерку.
ü Чтобы найти целое надо мерку умножить на количество мерок
Для обучения можно использовать следующие виды заданий:
1. Реши задачу, обосновывая выбор арифметического действия.
Задача. «В машину могут сесть 5 человек. Сколько надо машин, чтобы разместить 35 человек?».
ü Сформулируй тройку величин на естественном языке.
ü Сформулируй тройку величин на языке схемы.
ü Дополни вспомогательные модели количественными характеристиками к задаче:
| Количество человек в одной машине | Количество машин | Всего человек |
| Мерка | Количество мерок | Целое |
| 5ч. | ? | 35ч. |
2. По таблице составь задачу и две обратные ей. Разъясни взаимосвязь тройки величин.
| Число кусочков сахара в стакане | Число стаканов | Всего кусочков сахара |
| ? | ||
| ? | ||
| ? |
Покажем на примере простой текстовой задачи методику построения схематического чертежа и осуществим выбор арифметического действия на языке схемы.
«Цена одной книги 50 рублей. Сколько нужно заплатить за 5 таких книг?»
1. О каких объектах говорится в задаче? (О книгах.)
2. Что о них известно? (Цена одной книги равна 50 рублям; нужно заплатить за 5 таких книг.)
3. Что значит «таких» книг? (Цена этих книг одинаковая.)
4. Какие величины известны? (Цена, количество.)
5. Назовите данные величины на языке схемы. (Мерка, количество мерок.)
6. Что требуется найти? (Стоимость.)
7. Как называется стоимость на языке схемы? (Целое.)
8. Чему равна мерка? Количество мерок?
9. Начертите схему, расставьте количественные характеристики на схеме.
10. Когда схема готова, ученики повторяют по ней задачу, поясняя, что
обозначает каждое число и в чём заключается требование задачи. При выполнении подобных заданий дети начинают лучше и быстрее разбираться в математической структуре задачи, учатся читать зависимости, скрытые в схемах. Познакомив детей на примере простых задач с основными элементами схематического чертежа, которые помогают раскрыть связь между данными и искомым, можно готовить учащихся применять эти знания при решении составных задач. Для того чтобы выработать умение решать составные задачи на зависимость величин, необходимо обобщить знания детей об осуществлении поиска способа решения в соответствии с опорой на вспомогательную модель.
IV этап. Обучение решению задач, связанных пропорциональными величинами: задачи на нахождение четвёртого пропорционального, на пропорциональное деление и на нахождение неизвестного по двум разностям.
Рассмотрим виды деятельности учащихся при изучении процессов равномерного движения в 3 и 4классах.
| 3 класс | 4 класс |
| -Наблюдать зависимости между величинами: скоростью, временем, расстоянием с помощью графических моделей; -Фиксировать значения величин в таблицах; -Выявлять закономерности; -Строить соответствующие формулы зависимостей; -Строить формулу пути и использовать ее для решения задач; -Моделировать и анализировать условия задач с помощью таблиц. | -Систематизировать виды одновременного равномерного движения двух объектов: навстречу друг другу, в противоположных направлениях, вдогонку, с отставанием; -Исследовать зависимости между величинами при одновременном равномерном движении объектов по координатному лучу, заполнять таблицы; -Строить формулы скорости сближения и скорости удаления, применять их для решения задач; -Строить графики движения по словесному описанию, формулам, таблицам; -Читать, анализировать, интерпретировать графики движения, составлять по ним рассказы. |
Мы видим усложнение видов деятельности и уровня обобщения.
А теперь рассмотрим виды деятельности учеников при изучении процессов покупки и работы и сравним с видами деятельности при изучении процессов равномерного движения.
| Процесс покупки. | Процесс работы. |
| -Наблюдать зависимости между величинами: стоимостью, ценой и количеством товара с помощью таблиц -Выявлять закономерности и строить соответствующие формулы зависимостей -Строить формулу стоимости и использовать ее для решения задач на покупку товара -Устанавливать аналогию между задачами на движение и задачами на стоимость -Моделировать и анализировать условия задач с помощью таблиц -Записывать заданную программу действий с помощью числового выражения | -Наблюдать зависимости между величинами: объемом выполненной работы, производительностью, временем работы с помощью таблиц -Выявлять закономерности -Строить соответствующие формулы зависимостей -Строить формулу работы и использовать ее для решения задач -Моделировать и анализировать условия задач с помощью таблиц -Выявлять аналогию между задачами на движение, стоимость, работу, строить общую формулу произведения |
Данные виды деятельности аналогичны при изучении всех процессов, что способствует формированию общего способа решения задач на нахождение произведения, т. е. выявлять аналогию между задачами на движение, стоимость, работу, строить общую формулу произведения; определять общие методы решения задач на движение, покупку товара, работу. Подводить под формулу произведения различные зависимости, описывающие реальные процессы окружающего мира. Классифицировать простые задачи изученных типов по виду модели и устанавливать на этой основе общие методы к решению составной задачи, применять их для решения составных задач в 2-5 действий. Строить формулы зависимостей между величинами по данным таблиц, текстовым условиям задач. Решать задачи по изученным формулам.
Рассмотрим рассуждения учащихся в процессе решения составных задач на пропорциональную зависимость.
Не нашли, что искали? Воспользуйтесь поиском: