Тема 1. Элементы линейной алгебры

Матрицы. Действия над матрицами. [3, §1]. Определители. Свойства определителей. [3, §2]. Невырожденные матрицы. Обратная матрица. [3, §3]. Ранг матрицы. [3, §3]. Системы линейных алгебраических уравнений. Решение систем линейных алгебраических уравнений по правилу Крамера, с помощью обратной матрицы, методом Гаусса. [3, §4].

Пример 1. Дана матрица . Найти .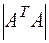

Решение: Транспонируем матрицу :
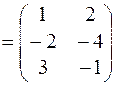. Матрица имеет размерность 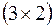, матрица имеет размерность . Значит, произведение этих матриц возможно, и матрица будет иметь размерность .

.

Определитель матрицы найдем, воспользовавшись «правилом треугольников»:

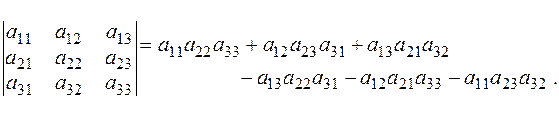
Пример 2. Решить систему уравнений 1) по правилу Крамера; 2) с помощью обратной матрицы; 3) методом Гаусса.

Решение: 1. Найдем главный определитель системы:

Так как , то система имеет единственное решение.

Найдем вспомогательные определители системы:

; ; .

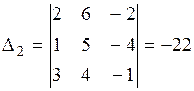Значит, ; ; .

2. Запишем заданную систему уравнений в матричной форме , где – матрица коэффициентов системы; – столбец неизвестных; 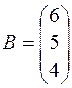– столбец свободных членов.

Тогда , где – обратная матрица к матрице .

Так как , то существует. Обратная матрица может быть найдена по формул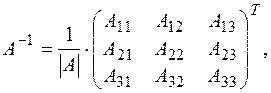е где 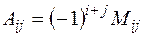– алгебраическое дополнение элемента матрицы ; – минор элемента матрицы , то есть определитель, полученный из матрицы путем вычеркивания -й строки и -го столбца.

Определитель второго порядка может быть найден по формуле .

Находим алгебраические дополнения элементов матрицы :

;
; .

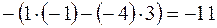Аналогично ; ; ; ; ; .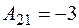

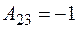Значит, .

Тогда

,

то есть , , .

3. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду:

.

Откуда следует, что ранги матриц и равны , то есть система уравнений совместна. Число неизвестных , значит, система уравнений имеет единственное решение.

Перейдем от полученной ступенчатой матрицы к системе, эквивалентной заданной:

Решая систему «снизу вверх», получаем, что , , .

Не нашли, что искали? Воспользуйтесь поиском: