Тема 4. Аналитическая геометрия в пространстве

Уравнения плоскости в пространстве. Основные задачи о плоскости. Уравнения прямой линии в пространстве. Основные задачи о прямой линии. Прямая и плоскость в пространстве. Поверхности второго порядка. [3, §12].

Пример 8. Даны точки ; ; ; . Найти: 1) длину отрезка ; 2) уравнения прямых и 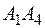; 3) угол между прямыми и 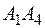; 4) уравнение плоскости 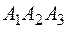; 5) угол между прямой 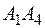и плоскостью 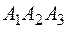; 6) уравнения высоты, опущенной из точки на плоскость .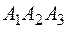

Решение:

1. Расстояние между точками и находится по формуле .

В данном случае .

2. Уравнения прямой, проходящей через две заданные точки пространства и имеют вид .

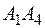Тогда уравнения прямой : или , уравнения прямой : или .

3. Острый угол между прямыми линиями, заданными уравнениями и определяется по формуле: .

Из уравнения прямой : , , ; из уравнения прямой 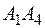: , , . Следовательно,

, .

4. Уравнение плоскости, проходящей через три заданные точки 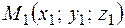, , имеет вид .

Тогда уравнение плоскости : ;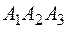

; .

5. Острый угол между прямой линией и плоскостью определяется по формуле: .

Из уравнения прямо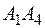й : , , ; из уравнения плоскости : , , .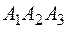

Следовательно, , .

6. Уравнения высоты, опущенной из точки на плоскость 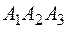имеют вид: , где , , (координаты точки ), – направляющий вектор искомой прямой.

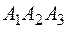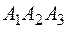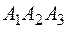Так как эта прямая перпендикулярна плоскости , то за вектор можно принять вектор нормали плоскости . Так как (, , – коэффициенты из общего уравнения плоскости ), то .

Значит, искомые уравнения имеют вид .

Не нашли, что искали? Воспользуйтесь поиском: