
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 2. Элементы векторной алгебры
Векторы. Линейные операции над векторами. Проекция вектора на ось. Модуль вектора. Направляющие косинусы. [3, §5]. Скалярное произведение векторов. Свойства скалярного произведения. Выражение скалярного произведения через координаты. Некоторые приложения скалярного произведения. [3, §6]. Векторное произведение векторов. Свойства векторного произведения. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения. [3, §7]. Смешанное произведение векторов. Свойства смешанного произведения. Выражение смешанного произведения через координаты. Некоторые приложения смешанного произведения. [3, §8]. Собственные векторы и собственные значения матриц. [4, гл. V, §4].
Пример 3. Дано: 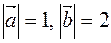 ,
, 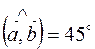 , векторы
, векторы 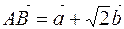 и
и 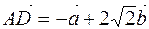 составляют стороны параллелограмма
составляют стороны параллелограмма 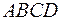 . Найти: 1) длины диагоналей параллелограмма
. Найти: 1) длины диагоналей параллелограмма 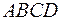 ; 2) острый угол между диагоналями параллелограмма
; 2) острый угол между диагоналями параллелограмма 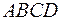 ; 3) площадь параллелограмма
; 3) площадь параллелограмма 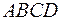 .
.
Решение: Сделаем схематический чертеж:
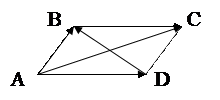

1. Найдем длины диагоналей параллелограмма 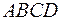 как длины векторов
как длины векторов 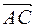 и
и 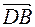 .
.
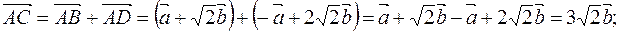
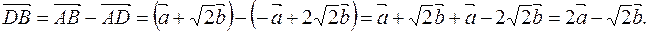
Скалярный квадрат вектора равен квадрату модуля этого вектора, то есть 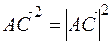 и
и 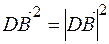 . Имеем
. Имеем
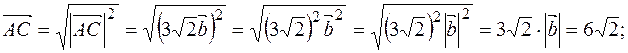
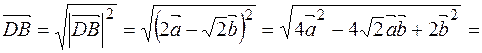
 .
.
2. Острый угол между диагоналями параллелограмма 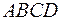 найдем по формуле
найдем по формуле 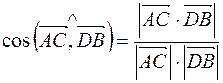 .
.
Находим скалярное произведение векторов  и
и  :
:
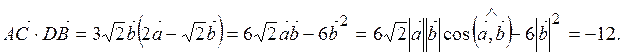
Значит, 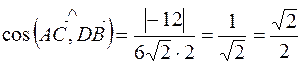 и
и 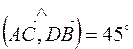 .
.
3. Площадь параллелограмма 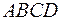 найдем по формуле
найдем по формуле  .
.
По свойствам векторного произведения имеем
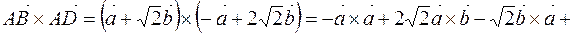

Значит, 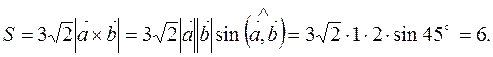
Пример 4. Даны точки 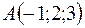 ;
; 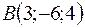 ;
; 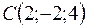 ;
; 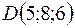 . Требуется: 1) записать векторы
. Требуется: 1) записать векторы  ,
,  ,
, 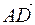 в ортонормированном базисе; 2) найти длины векторов
в ортонормированном базисе; 2) найти длины векторов  ,
,  ,
, 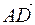 ; 3) показать, что векторы
; 3) показать, что векторы  ,
,  ,
, 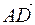 образуют базис трехмерного пространства; 4) найти острый угол между векторами
образуют базис трехмерного пространства; 4) найти острый угол между векторами  и
и 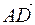 ; 5) найти алгебраическую проекцию вектора
; 5) найти алгебраическую проекцию вектора  на вектор
на вектор 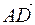 ; 6) найти площадь треугольника
; 6) найти площадь треугольника 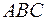 ; 7) найти объем пирамиды
; 7) найти объем пирамиды 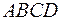 .
.
Решение: 1. Если 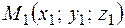 ,
,  , то вектор
, то вектор  .
.
В данном случае имеем 
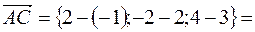
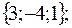
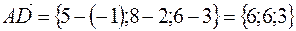 .
.
Значит, 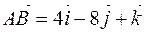 ,
,  ,
, 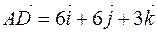 .
.
2. Длина вектора 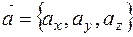 может быть найдена по формуле
может быть найдена по формуле  .
.
Имеем 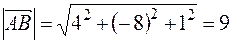 ;
; 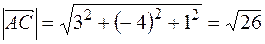 ;
;
 .
.
3. Покажем, что векторы  ,
,  ,
, 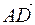 образуют базис трехмерного пространства. Для этого найдем определитель, составленный из координат этих векторов:
образуют базис трехмерного пространства. Для этого найдем определитель, составленный из координат этих векторов:
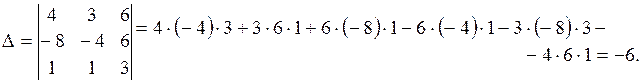
Так как  , то векторы
, то векторы  ,
,  ,
, 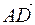 образуют базис трехмерного пространства.
образуют базис трехмерного пространства.
4. Острый угол между векторами  и
и 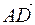 найдем по формуле
найдем по формуле  .
.
Скалярное произведение векторов  и
и 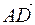 найдем, используя формулу:
найдем, используя формулу: 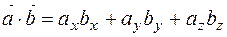 , где
, где 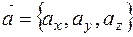 ,
, 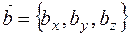 . В данном случае
. В данном случае 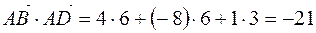 .
.
Тогда 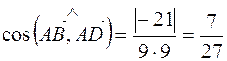 и
и 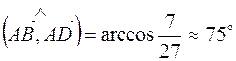 .
.
5. Алгебраическую проекцию вектора  на вектор
на вектор 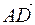 найдем по формуле
найдем по формуле  .
.
Так как 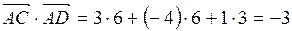 , то
, то  .
.
6. Площадь треугольника 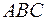 найдем по формуле
найдем по формуле 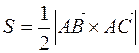 .
.
Векторное произведение векторов 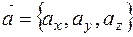 и
и 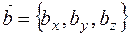 можно найти по формуле
можно найти по формуле 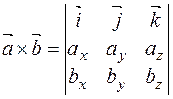 .
.
В данном случае 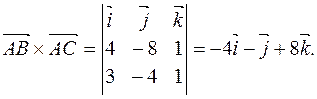
Тогда 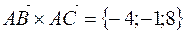 ,
, 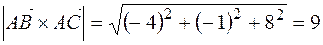 . Значит,
. Значит, 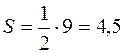 .
.
7. Объем пирамиды 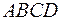 найдем по формуле
найдем по формуле 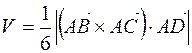 .
.
Смешанное произведение векторов 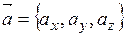 ,
, 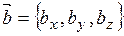 и
и  можно найти по формуле
можно найти по формуле 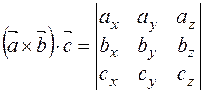 .
.
Тогда 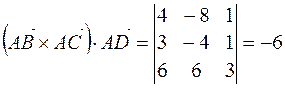 . Значит,
. Значит,  .
.
Пример 5. Найти собственные значения и собственные векторы матрицы 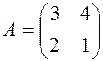 .
.
Решение: Собственные значения матрицы  находятся из уравнения
находятся из уравнения 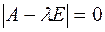 , где
, где  – единичная матрица того же порядка, что и матрица
– единичная матрица того же порядка, что и матрица  .
.
В данном случае 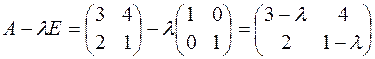 ,
,
 .
.
Решением уравнения 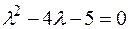 являются числа
являются числа 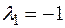 ,
, 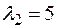 . Это и есть собственные значения матрицы
. Это и есть собственные значения матрицы  .
.
Собственный вектор  , соответствующий собственному значению
, соответствующий собственному значению 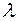 , определяется из системы уравнений
, определяется из системы уравнений 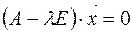 .
.
Находим собственный вектор 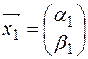 , отвечающий собственному значению
, отвечающий собственному значению 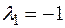 :
:  или
или 
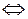

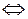
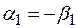 . Пусть
. Пусть  , тогда
, тогда 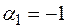 .
.
Значит, 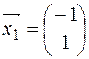 – собственный вектор, соответствующий собственному значению
– собственный вектор, соответствующий собственному значению 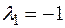 .
.
Находим собственный вектор 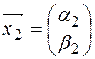 , отвечающий собственному значению
, отвечающий собственному значению 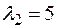 :
:  или
или 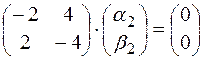
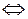
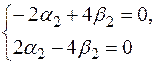
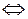
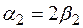 . Пусть
. Пусть  , тогда
, тогда 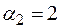 .
.
Значит, 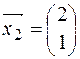 – собственный вектор, соответствующий собственному значению
– собственный вектор, соответствующий собственному значению 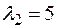 .
.
Не нашли, что искали? Воспользуйтесь поиском: