Тема 5. Введение в математический анализ

Числовые функции. График функции. Основные характеристики функции. Сложная функция. Основные элементарные функции и их графики. [3, §14]. Предел функции в точке. Односторонние пределы. Предел функции при . [3, §16]. Основные теоремы о пределах. Первый и второй замечательные пределы. [3, §17]. Непрерывность функции в точке и на отрезке. Точки разрыва функции и их классификация. Свойства функций, непрерывных на отрезке. [3, §19].

Пример 9. Найти пределы функций, не пользуясь правилом Лопиталя:

1) ; 2) ; 3) ;

4) ; 5) .

Решение:

1) .

2) .

Раскроем неопределенность . Так как и , то

.

3) .

Для раскрытия неопределенности разделим числитель и знаменатель на старшую степень :

, так как , , при .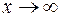

4) .

Для раскрытия неопределенности умножим числитель и знаменатель на выражение, сопряженное знаменателю:

.

5) .

Сделаем замену , тогда , . Так как 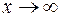, то .

Тогда

, так как – второй замечательный предел.

Пример 10. Дана функция Найти точки разрыва функции, если они существуют, и построить ее график.

Решение: Функции , , непрерывны на всей числовой прямой, поэтому заданная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, то есть в точках и .

Исследуем функцию на непрерывность в этих точках. Для этого найдем соответствующие односторонние пределы и значения функции.

Рассмотрим поведение функции при :

;

; .

Так как , то заданная функция непрерывна в точке .

Рассмотрим поведение функции при :

; .

Так как пределы и 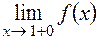конечны и не равны, то точка – точка разрыва I рода (функция в этой точке претерпевает «скачок» на единицы).

Сделаем чертеж:

Не нашли, что искали? Воспользуйтесь поиском: