Способы образования и задания на чертеже поверхностей вращения

Поверхности вращения (рис. 102) – цилиндрические, конические, сферические и другие – являются принадлежностью большого количества деталей машин и приборов самых разнообразных устройств, механизмов и изделий.

Это объясняется, с одной стороны, довольно широким распространением вращательного движения в технике и, с другой стороны, сравнительной простотой обработки поверхностей вращения на токарных и круглошлифовальных станках.

Поверхностью вращения называется такая поверхность, которая образуется при вращении какой-либо прямолинейной или криволинейной образующей вокруг неподвижной прямой линии – оси (рис. 103, а).

Проекциями образующей, например, плоскости кривой m, и оси вращения i поверхность вращения может быть задана на чертеже.

Для удобства построения чертежей ось вращения i обычно располагается перпендикулярно какой-либо плоскости проекций. В рассматриваемом примере ось вращения i (i ₂, i ₁) расположена перпенди-кулярно горизонтальной П₁ плоскости проекций, а криволинейная образующая m (m ₂, m ₁) расположена своей плоскостью параллельно фронтальной П₂ плоскости проекций.

Однако такой способ задания на чертеже поверхности вращения не дает полного представления о её конфигурации (очертании). Вместе с тем, зная характер движения образующей m относительно оси i, представляется возможным построение проекций очерков заданной поверхности вращения на фронтальную П₂ и горизонтальную П₁ плоскости проекций.

Известно, что любая образующая – прямая или кривая линия – представляет собой некоторую совокупность множества точек. При вращении образующей вокруг оси каждая из точек этого множества будет совершать движение по окружности, плоскость которой располагается перпендикулярно оси вращения. Окружность, по которой каждая из точек образующей поверхности вращается вокруг оси, называют параллелью поверхности вращения. Наибольшую параллель называют экватором. Каждая точка поверхности имеет свою параллель.

Выделим на чертеже (рис. 103, б) некоторые из точек криволинейной образующей m. Например, точки А (А₂, А₁) и В (В₂, В₁), ограничивающие криволинейную образующую на высоте относительно горизонтальной П₁ плоскости проекций, и точки 1 (1₂, 1₁), 2 (2₂, 2₁), имеющие соответственно наименьший и наибольший радиусы вращения вокруг оси i.

Траектории вращения точек А, В, 1 и 2 представляют собой окружности (параллели) (рис. 104, а), центры которых располагаются на оси вращения i. В связи с тем, что ось вращения поверхности расположена на чертеже перпендикулярно горизонтальной П₁ плоскости проекций, то параллели точек А, В, 1 и 2 располагаются на чертеже следующим образом:

- фронтальные проекции параллелей – точки А (А₂-А₂), точки
В (В₂-В₂), точки 1 (1₂-1₂) и точки 2 (2₂-2₂) представляют собой прямые линии, расположенные перпендикулярно проекции i ₁ оси вращения;

- горизонтальные проекции параллелей этих же точек представляют собой окружности, центры которых совпадают с проекцией i ₁ оси вращения.

И так как плоскости окружностей – параллелей точек располагаются перпендикулярно оси вращения, а последняя в свою очередь расположена на чертеже перпендикулярно горизонтальной П₁ плоскости проекций, то параллели всех точек образующей m проецируются на горизонтальную плоскость проекций без искажения – в натуральную величину и определяют сочетание поверхности вращения на этой плоскости проекций.

Отсюда следует вывод о том, что проекции параллелей определяют очертание поверхности вращения на той плоскости проекций, которая перпендикулярна оси вращения.

Если теперь на чертеже соединить плавной кривой линией крайние правые точки фронтальных проекций параллелей, например, точки и другие из множества точек, принадлежащих образующей m поверхности, то получим новую m ₂ проекцию образующей m вращения (рис. 104, б). Это будет соответствовать повороту в пространстве заданной образующей m поверхности на угол, равный 180°.

С другой стороны, подобное очертание поверхности вращения получается при рассечении её плоскостью, проходящей через ось i и расположенной параллельно фронтальной П₂ плоскости проекций.

Сечение поверхности вращения плоскостью, проходящей через её ось, называется меридианом, а секущая плоскость – меридиональной.

Поверхность вращения симметрична относительно любой меридиональной плоскости, а все меридианы поверхности равны между собой. Через точку, лежащую на поверхности вращения, можно провести только один меридиан.

Если же меридиональная плоскость параллельна плоскости проекций, то она называется главной меридиональной плоскостью, а сечение поверхности вращения этой плоскостью – главным меридианом.

Проекция главного меридиана определяет очертание (контур) поверхности вращения на той плоскости проекций которой параллельна ось вращения.

Плоскости главного меридиана и экватора определяют видимость точек поверхности вращения на соответствующих плоскостях проекций.

Следовательно, любая поверхность вращения может быть задана на чертеже не только проекциями её образующей и оси вращения, но и проекциями главного меридиана и параллелей (рис. 105, б). Сопоставляя очертания (контуры) поверхности вращения на плоскостях проекций, не трудно представить (риc. 105, б) и наглядное изображение фигуры в пространстве.

Рассмотрим пример образования поверхности вращения с использованием в качестве образующей прямой линии (рис. 106, а), которая в пространстве располагается так, что она не параллельна и не пересекается с осью вращения, то есть является по отношению к ней скрещивающейся прямой.

По-прежнему ось вращения i (i ₂, i ₁) поверхности располагается перпендикулярно горизонтальной П₁ плоскости проекций. На чертеже образующая – прямая П – ограничена отрезком А-В.

При вращении отрезка А-В (рис. 106, б) вокруг оси i траектории движения точек А (А₂, А₁) и В (В₂, В₁) представляют собой окружности – параллели, проецирующиеся на горизонтальную П₁ плоскость проекций в натуральную величину.

На чертеже горизонтальные проекции параллелей точек А и В совпадают. Это означает, что радиусы параллелей этих точек одинаковые – равны между собой.

Фронтальные проекции параллелей точек А и В представляют собой прямые линии, проходящие через точки А₂ и В₂ в направлении, перпендикулярном проекции i ₂ оси вращения, и должны соответствовать натуральной величине диаметров параллелей этих точек.

Для определения их размеров отмечаем на горизонтальной плоскости проекции точек пересечения параллельных точек А и В со следом главной меридиональной плоскости поверхности. Затем при помощи линий связи, проведённых через эти точки, находим положения их

Рис. 105

Рис. 106

проекций на соответствующих фронтальных проекциях параллелей точек А и В.

Отрезки и представляют собой фронтальные проекции параллельных точек А и В, равные по своим значениям натуральной величине их диаметров.

Рассматривая на чертеже (рис. 107, а) горизонтальную А₁–В₁ проекцию отрезка А-В, нетрудно установить, что среди множества точек образующей имеется только одна точка с минимальным радиусом параллели. Для определения положения горизонтальной проекции этой точки достаточно из точки i₁ опустить перпендикуляр на прямую А₁–В₁. Это построение выполнено на том основании, что параллель любой точки образующей А–В проецируется на горизонтальную плоскость проекций в натуральную величину.

Рис. 107

Основание этого перпендикуляра – точка С₁ и есть горизонтальная проекция точки С отрезка А-В с минимальным радиусом параллели.

Теперь раствором циркуля, равным отрезку i₁-C₁, проведем эту параллель и отметим точки ₁ и ₁ пересечения параллели со следом меридиональной плоскости поверхности.

Для построения фронтальной ₂- ₂ проекции этой параллели вначале, на основании признака принадлежности точки С отрезку А-В, строим ее фронтальную С₂ проекцию и проводим через неё прямую в направлении, перпендикулярном проекции i ₂ оси вращения, а затем при помощи линий связи, проведенных через точки ₁, ₁ до пересечения с этой прямой, определяем их расположение на фронтальной плоскости проекций. Получаем точки ₂ и ₂.

Отрезок ₂- ₂ и есть фронтальная проекция параллели точки С отрезка А-В с минимальным радиусом вращения.

На рис. 107, б представлено наглядное изображение отрезка А-В и параллелей его точек А, В, С.

Подобным образом (рис. 108, а) можно построить на горизонтальной и фронтальной плоскостях проекций параллелей некоторого множества точек отрезка А-В образующей.

Рис. 108

При этом необходимо обратить внимание на то, что главная меридиональная плоскость определяет видимость проекций точек отрезка А-В на фронтальной плоскости проекций. Точкой же видимости проекций А₂-В₂ отрезка образующей является точка пересечения горизонтальной проекции А₁-В₁ со следом главной меридиональной плоскости – точка Д₁.

На основании признака принадлежности точки Д отрезку А-В построена на чертеже её фронтальная Д₂ проекция.

Если теперь (рис. 108, б) соединить плавной кривой линией крайние правые и крайние левые точки фронтальных проекций параллелей этого множества, то получим очертание (проекцию контура) главного меридиана поверхности вращения, представляющего собой гиперболу.

В связи с этим поверхность, полученная вращением скрещивающейся прямой – образующей вокруг неподвижной оси, называется однополостным гиперболоидом вращения.

На рис. 109, а представлено наглядное изображение – прямоугольная диметрическая проекция однополостного гиперболоида вращения.

При использовании в качестве образующей поверхности вращения прямой (рис. 109, б), расположенной в пространстве параллельно оси вращения, образуется цилиндр вращения. Каждая из точек образующей, например, точки А, С, В прямой m, совершают вращательное движение вокруг оси i. Траектории их движения представляют собой окружности – параллели, плоскости которых перпендикулярны оси вращения. Если ось вращения цилиндра перпендикулярна какой-либо плоскости проекций, он называется прямым, а его поверхность является проецирующей.

Рис. 109

На комплексном чертеже (рис. 110) цилиндр вращения задан проекциями своего контура на фронтальной и горизонтальной плоскостях проекций. В нашем примере главный меридиан прямого цилиндра вращения представляет собой прямоугольник, а горизонтальная проекция – окружность, являющуюся геометрическим местом горизонтальных проекций параллелей точек образующей поверхности.

Коническая поверхность вращения – конус вращения (рис. 111, а) образуется вращением прямолинейной образующей, пересекающейся с осью вращения в постоянной точке. При заданном на чертеже (рис. 111, б) расположении оси вращения конус вращения называется прямым.

Главным меридианом такого конуса является треугольник, вторая проекция его представляет собой проекцию окружности основания.

Рис. 110

Широкое распространение получило использование в качестве криволинейных образующих поверхностей вращения плоских кривых линий (рис. 112, а), в частности, окружностей и их дуг, эллипсов, парабол, гипербол.

Вращением окружности вокруг оси, проходящей через её центр, образуется сферическая поверхность вращения – сфера. На комплексном чертеже (рис. 112, б) сфера задается проекциями двух окружностей равного диаметра.

Рис. 111

Рис. 112

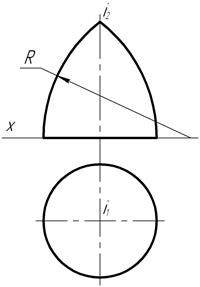
Рис. 113 Рис. 114

Вращением окружности (рис. 113) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через её центр, образуется тор. При этом, если ось вращения проходит так, как показано на чертеже, вне окружности, тор называется кольцом.

На чертеже (рис. 114) изображена поверхность, образующей которой является дуга окружности радиуса R. Такая поверхность вращения называется глобоидом.

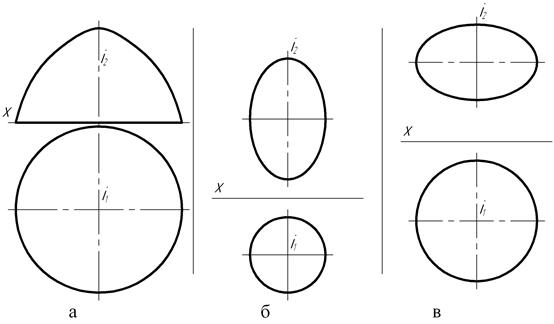
Рис. 115

Вращением параболы (рис. 115, а) вокруг её оси образуется поверхность, которая называется параболоидом вращения. Параболоид вращения используется в качестве отражающей поверхности в прожекторах и фарах автомобилей для получения параллельного светового пучка.

При вращении эллипса (рис. 115, б, в) вокруг одной из его осей – большей или меньшей, образуется эллипсоид вращения.

Если осью вращения является большая ось эллипса (рис. 115, б), то эллипсоид вращения называется вытянутым, а если меньшая ось
(рис. 115, в), то эллипсоид вращения называется сжатым или сфероидом. В частности, земной шар по форме близок к сфероиду.

Использованием в качестве образующей поверхности вращения плоской кривой линии – гиперболы получают гиперболоид вращения (рис. 116). При этом различают: однополостный и двуполостный гиперболоиды вращения.

Вращение гиперболы вокруг её мнимой оси (рис. 116, а) образуется однополостный гиперболоид вращения. На наглядном изображении помимо гиперболоида показан его асимптотический конус вращения, образованный вращением асимптот гиперболы, являющихся образующими гиперболы. Во внешней части этого конуса и расположен однополостный гиперболоид вращения.

Рис. 116 Рис. 117

Двуполостный гиперболоид вращения (рис. 116, б) образуется вращением гиперболы вокруг её действительной оси. На наглядном изображении действительная ось гиперболоида расположена перпендикулярно горизонтальной плоскости проекций. При вращении асимптот гиперболы вокруг действительной оси получают асимптотический конус вращения, во внутренней части которого и расположен двуполостный гиперболоид вращения.

В качестве образующих поверхности вращения могут быть использованы не только плоские, но и любые пространственные кривые линии.

Рассматривая в целом особенности образования и задания на чертеже поверхностей вращения, можно сделать вывод о том, что меридианы и параллели составляют каркас поверхности вращения
(рис. 117), то есть представляют собой множество линий, заполняющих поверхность вращения так, что через каждую точку этой поверхности в общем случае проходит только одна линия этого множества.

Это положение позволяет сформулировать признак принадлежности точки поверхности вращения: если точка принадлежит поверхности вращения, то через неё можно провести только одну параллель и только один меридиан.

Не нашли, что искали? Воспользуйтесь поиском: