Бөлімдері әр түрлі бөлшектер мен аралас сандарды қосу және алу.

а) ең үлкен бөлімі ең кіші ортақ бөлімі болып табылады:

1) + 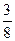, 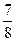- 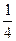; 2) 1 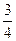+ 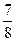, 4 -

б) ең үлкен бөлімі ең кіші ортақ бөлімі болып табылмайды:

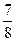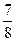1) + , - ; 2) 1 + , 1 -

Бөлімдері әр түрлі бөлшектерді өосу және алу амалын орындаған кезде, ақыл есі кем оқушыларға қиындық туғызады. Себебі, есепті шығармас бұрын бөлшекті ең кіші ортақ бөлімге келтіру керек. Осыған байланысты оқушылар зейінін қосымша операцияға ауыстыра алмайды (өрнектің жазуы ұзарып кетеді - өрнекке теңестіру таңбасын қойып, бірнеше рет көшіру керек). Бұл оқушылардан зейіннің шоғырлануын талап етеді. Ал бізге белгілі, интеллектісі бұзылған оқушылардың зейіні тұрақсыз болып келеді. Мұндай қателікті жібермес үшін, оқушылар дәптерге жазбай тұрып, өрнектеуді қалай жазатынын ауызша айту қажет: 1) бөлшекті ең кіші ортақ бөліміне келтіру; 2) әрекетті орындау; 3) мүмкін болса, жауаптарды түрлендіру.

Аралас сан мен бөлшекті қосқан кезде оқушылардың назарын шыққан нәтижесіне және әр қосылғышқа аударып, бүтін сандардың қажеттілерін салыстыру керек.

Бөлшектерді қосу және алуды өмірлік тәжірибелік тапсырмалар мен жаттығуларды байланыстырып, ауызша шығаруға да болады.

Мысалы «Көйлек тігу үшін 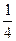м ақ және 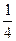м көк тесманы алды. Көйлек тігу үшін қанша тесма кетті?»

Бұл кезеңде оқушыларға қосу және алу мысалдарының белгісіз компоненттерін табуға арналған есептерді шығарған және бөлшек пен бүтін сандарды қосып, алғандағы белгісіз компонентердің орнын ауыстырған жөн.

Оқушылар арифметикалық әрекетінің орын ауыстыру және салыстыру заңдары тек қана бүтін сандарға ғана емес, сонымен қатар бөлшек сандарға да ортақ екеніне көз жеткізулері керек.

Жай бөлшектерді көбейту және бөлу. VIII типтегі мектепте тек қана бөлшек пен аралас санның бүтін санға көбейту мен бөлуді қарастырады.

Бұл әрекетті оқыту қосу мен алуды оқытқан кезде параллельді жүргізіледі.

Бөлуді қарастырмас бұрын біз алдымен бөлшекті бүтін санға көбейтуді, ал содан кейін бөлу әдістерін түсіндіруді қарастырамыз.

Оқушыларға бөлшекті бүтін санға көбейтуді таныстырмай тұрып, бүтін сандарды көбейтуді қайталау қажет.

Бөлшекті бүтін санға көбейтуді қарастырған кезде әр түрлі жағдайларды, яғни оның қиындық деңгейімен анықталған әр түрлі жағдайлар қатарын қадағалау қажет.

1. Бөлшекті бүтін санға көбейту.

2. Аралас санды бүтін санға көбейту.

Бөлшекті бүтін санға көбейтуді түсіндіретін дайындық тапсырмалары келесілер: бүтін сандарды көбейту кезінде көбейтуді қосумен орынауыстырып жазу жаттығулары болып табылады. Мысалы: 7×3=21 көбейтуді қосу амалымен ауыстыру 7+7+7=21, көбейту әрекетін (бірінші көбейткіш бөлшек - 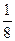; екінші көбейткіш – бүтін сан) қосу әрекетімен ауыстыру. Есептің алымы мен бөліміне және бірінші көбейткішке назар аудару қажет. Мынадай сұрақтар арқылы: «Көбейту кезінде бөлшектің бөлімі өзгереді ме? Бөлшектің алымымен не болды?» - оқушылар қорытындыға келеді, алымы 3 есеге көбейді, ал бөлімі сол күйінде қалды. Бөлшекті бүтін санға көбейту ережесін қорытындылау тек бір мысал арқылы қарастыру жеткіліксіз болады, тағы бірнеше есептерді қарастыру қажет.

Берілген есептердің дұрыс жауабын суреттер арқылы көрсету керек.

Бөлшекті бүтін санға көбейтуді меңгергеннен кейін оқушыларға алымын бүтін санға көбейтпей тұрып, осы сандарды бөлімімен салыстыруды көрсету керек.

Интеллектуалды жеіспеушілігі бар балалар есепті шығару барысында рационалды тәсілдерді өте сирек қолданады. Әдетте олар өздеріне белгілі стереотипті тәсілдерді қолданады.Сондықтан мұғалім оқушылардан сирек болса да рационалды тәсілдерді қолдануды талап ету керек.

Аралас санды бүтін санға көбейтуді түсіндірмей тұрып, өлшеу кезінде көлемді алған көбейткен сандарды қайталау қажет.

Аралас санды бүтін санға көбейткен кезде оқушылардың назарын аралас санды бөлшек түрінде жазып, ал содан кейін барып көбейтуді бүтін санға бөлшекті көбейту ережесіне сүйене отырып шығаруға аудару керек.

Бұл алу тәсілінің жетіспеушіліг: алымындағы сан өте үлкен. Егер алымындағы сан үлкен болса, есепті шығарған кезде қиындықтар туғызады.. Бірақ бұл тәсілдің жақсы да жері бар: болашақта оқушылар аралас санды бүтін санға бөлу тақырыбымен танысқан кезде, әрекетті жасамас бұрын олар аралас санды теріс бөлшек ретінде өрнектеуде қиналмайды.

Жақсы оқитын оқушыларға аралас санды бүтін санға көбейтудің екінші тәсілін көрсетсе болады: бөлшекті бүтін санға көбейту. Бұл жағдайда бүтін сан бүтінге көбейтіледі, алынған жауап бүтін санмен жазылады, содан кейін санның бөлшек бөлігі бөлшекті бүтін санға көбейту ережесіне сүйене отырып көбейтіледі.

«Бөлшекті бүтін санға көбейту» тақырыбын оқытқан кезінде бөлшек бірнеше есе көбейетін жағдайындағы есептер мен мысалдарды шығарған жөн.Оқушыларға × 3 мысалын әр түрлі етіп оқуға болатындығын көрсету керек: -ні 3-ке көбейтеміз, -ні 3 есе көбейтеміз, және 3 жауабын табу керек, және 3 көбейткіштері, жауабын табу. × 3 = есебін шығарғаннан кейін жауабы мен бірінші көбейткішті салыстыру керек: -ден 3 есе үлкен, -дан 3 есе кем.

Бірінші көбейткіште алымы немесе бөлімі белгісіз есептерді жығарру қажет: × 2= . Бұдан да күрделі есептерді ұсынуға болады. Мысалы, алымыда, бөлімі де белгісіз бөлшекті бүтін санға көбейту, бөлшегін 3 есе көбейт.

Бөлшекті бүтін санға көбейтуді былай орындау қажет:

1. Бөлшекті бүтін санға бөлуді алдын ала қысқартусыз орындау.

2. Аралас санды бүтін санға алдын ала қысқартусыз орындау.

3. Бөлуді қысқарту арқылы орындау.

Оқушыларға бөлшекті немесе аралас санды бүтін санға бөлу жағдайлары кезінде алдын ала қысқарту әрекетті орындау процесін жеңілдетеді.

Бақылау мен нақты әрекеттер кезінде оқушылар мынадай шешімге келеді: бөлшекті бүтін санға бөлген кезде бөліктер майдаланады, ал сандары өзгермейді. Мысалы, жарты алманы алайық және сол жартыны тағы 2 бірдей бөлікке бөлейік (: 2). Алманың 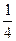бөлігі шығады. Былай жазамыз: : 2 = 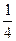. Әр оқушы міндетті түрде өз бетінше дөңгелектің (кесінді, сызық) жартысын тағы 2 бірдей бөлікке бөліп, бөлудің нәтижесін жазуы керек.

Ары қарай бөлуді қарастырамыз, мысалы, 3 бірдей бөлікке бөлу: : 3 = Оқушылар бөлу кезінде тоғыз бөлік шыққанын және оның сандарының өзгермегендігін көреді. Бөлгіш пен бөлінгіштің алымы мен бөлімін салыстырамыз: бөлімі 3 есеге көбейді, ал алымы өзгерген жоқ. Осыдан қорытынды шығаруға болады: бөлшекті бүтін санға бөлу үшін, бөлімін сол санға көбейтіп, алымын сол күйінде қалдырамыз. Осыдан кейін оқушылар тағы бірнеше мысалдарды шығарып, жауаптары дұрыс екеніне көз жеткізулері қажет.

Бөлшекті бүтін санға бөлуді бөлшекті бүтін санға көбейтумен теңестіру қажет. Осыдан жауаптарын және бірінші көбейткіш пен бөлгішті салыстыру керек. Бұны оқушылар бір қорытындыға келу үшін орындау қажет: бөлшекті бүтін санға көбейткен кезде оның жауабы бірінші көбейткіштен екінші көбейткіш қанша бірлікті құраса соған сәйкес болу керек.

Аралас санды бүтін санға бөлген кезде аралас сан теріс бөлшекке айналып, бөлу әрекеті бөлшекті бүтін санға бөлу ережесімен шығарылады.

Жақсы оқитын оқушыларға бөлу әрекетінің ерекше жағдайымен таныстырып өткен жөн болады. Егер аралас санның бүтін бөлігі бөлгішке бөлінсе, онда аралас сан теріс бөлшекке айналмай қалады, мысалы: 2 : 2 = 1 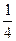. Ең алдымен бүтін бөлігін бөліп, жауабын жазу керек, содан кейін бөлшек бөлімін бөлшекті бүтін санға бөлу ережесіне сүйене отырып бөлу керек.Жай бөлшектерді барлық төрт әрекет арқылы шешуді оқытқаннан кейін одан да күрделі жақшалармен есептерді шығаруды үйренеді.

Санның бір және бірнеше бөліктерін табу. Берілген тақырып «Бөлшектерді алу» тақырыбынан кейін оқытылады.

Жаңа түсінікті түсіндіру үшін тәжірибелік есепті шығарудан бастай керек, мысалы: «Ұзындығы 80см тақтаның 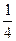бөлігін кеті. Тақтаның кескен бөлігінің ұзындығы неше?» Бұл тапсырманы оқушыларға заттық көрнекіліктерде көрсету қажет. Ұзындығы 80см планканы аламыз. Оның ұзындығын метрлік сызғышпен өлшейміз, содан кейін оқушылардан осы планканың 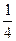бөлігін қалай табу керектігін сұраймыз. Оқушылар планканы төрт бірдей бөлікке бөліп төрттен бір бөлігін кесу керек екенін біледі. Планканың кесіп алынған бөлігін өлшейді. Оның ұзындығы 20см тең келеді. «20см деген ұзындықты қалай таптыңдар?»- деп сұрайды мұғалім оқушылардан. Бұл сұраққа жауап берген кезде кейбір оқушыларда қиындықтар туғызады, сол үшін планканы 4 бірдей бөлікке бөліп, ары қарай 80см-ді 4 бірдей бөлікке бөледі. Бұл есептің шығару жолын жазып көрсетейік: 80см-дің 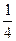бөлігі 80см: 4=20см болады.

Санның бірнеше бөлігін табуды VIII типтегі мектепте екі арифметикалық әрекеттер көмегімен шығарады. Бірінші әрекетте санның бір бөлігі анықталады, екіншісінде – бірнеше бөлігі анықталады.

Санды оның бір бөлігі арқылы табу. Берілген тақырыпқа жұмысты жүргізуді таза тәжірибелік мазмұны бар есептермен байланыстыру керек. Мысалы: «Бізге белгілі, теңге 50 теңгені құрайды. Барлық сан неге тең? (бүтін тиында қанша теңге бар?)» 1 теңге 100 тыннан тұратынын оқушылар біледі. Егер бұл белгілі болса, яғни оның бөлігі неге тең екенін білсек, онда белгісіз санды табуға болады. Теңгенің бөлігі, яғни 50 тиынды 2-ге көбейтеміз.

Осылайша оқушылардың өмірлік тәжірибесінен және бақылаудан жинақталған тағы бірнеше есептеп қатарын қарастырайық.

«25см 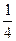м-ді құрайды. 1м-де қанша сантиметр бар?»

Шешімі: 25см × 4 = 100см.

«Көйлек тігу үшін 3м матаны құртты. Бұл барлық сатып алынған матаның бөлігін құрайды. Қанша метр мата сатып алынды?»

Шешімі: 3м × 3 = 9м – бұл барлық сатып алынған мата.

Енді 9 м-дің бөлігі 3 екенін тексеруіміз қажет. 9 м-дің бөлігін біз табуды білеміз. 9м: 3 = 3м. 3м – бұл барлық сатып алынған матаның 9 м-дің бөлігі. Есеп дұрыс шығарылды.

Оқушылар санды бөлік арқылы табуды үйренгеннен кейін, есептің жауабын шығарылған есептердің жауаптарымен теңестіру қажет.

Тәжірибелер көрсеткендей теңестеруді тиімді жүргізу үшін фабуласы бірдей есептерді шығаруды ұсынады:

«Сыныпта барлығы 16 оқушы бар. Қыздар оқушылардың 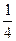бөлігін құрайды. Сыныпта қанша қыз бар?»

Шешімі: 16 оқушыдан 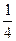табу. 16оқушы: 4 = 4оқушы.

Жауабы: Сыныпта 4 қыз бар.

«Сыныпта 4 қыз бар. Олар сыныптағы барлық оқушылардың 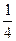бөлігін құрайды. Сыныпта барлығы қанша оқушы бар?»

Шешімі: 4оқушы × 4 = 16 оқушы.

Жауабы: Сыныпта барлығы 16 оқушы бар.

Не нашли, что искали? Воспользуйтесь поиском: