ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Лабораторная работа 1-4

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Определение момента инерции и проверка закона сохранения энергии с помощью маятника Максвелла

Цель работы: изучение законов сохранения энергии и определение момента инерции маятника Максвелла.

Теория

Маятник Максвелла состоит из тонкого металлического стержня — оси АВ с симметрично укрепленным на нем диском С (см. рис. 1). К концам стержня прикреплена крепкая капроновая нить, пропущенная через два отверстия в планке DE, которая укреплена на массивном штативе. На середине планки имеется винт, которым нить закрепляется в нужном положении после уравнивания длин отрезков нитей AD и BE. Нити тщательно, виток к витку, наматываются на стержень (от его концов к диску). Положение оси и расстояния, которые она проходит при движении маятника, измеряются по шкале К. После освобождения маятника он начинает движение из верхнего положения под действием силы тяжести: поступательное — вниз и вращательное — вокруг своей оси симметрии. Вращение, продолжаясь по инерции в низшей точке, когда нити уже размотаны, приводит вновь к наматыванию нитей на стержень, а следовательно, и к подъему маятника. Затем движение маятника вверх замедляется, он останавливается, снова начинается движение вниз и т. д. Такой колебательный характер движения вверх-вниз напоминает движение маятника, и поэтому устройство называется маятником Максвелла.

Цикл движения маятника Максвелла может быть подразделен на три стадии, а именно: спуск, удар, поднятие вверх. Схематически графики изменения скорости и ускорения точек оси маятника при его движении имеют вид, изображенный на рис. 2.

В соответствии с этим силы, действующие на маятник, должны быть подразделены на силы длительного действия (при спуске и поднятии) и силы кратковременного действия (удар). В первом случае эти силы не изменяются во времени, во втором — они резко нарастают и убывают.

Отметим, что удар при опускании маятника отличается от удара, например, шарика о плиту. Кинетическая энергия падающего тела (шарика) на первой стадии удара исчезает полностью, превращаясь в потенциальную энергию упругой деформации. При ударе маятника этого нет, остается кинетическая энергия его вращения, которая гораздо больше, чем кинетическая энергия поступательного движения перед ударом.

Экспериментальное ознакомление с движением маятника Максвелла состоит в наблюдении плоского движения (на всех трех стадиях движения маятника) и удара (вторая стадия). Получить полное аналитическое решение за весь цикл движения маятника не представляется возможным. В работе стадии движения рассматриваются отдельно одна от другой, используются предположения, которые упрощают рассмотрение вопроса. Естественно, это приводит к приближенным уравнениям, которые и применяются в экспериментальной части работы.

Теория движения маятника Максвелла. Движение маятника Максвелла является примером плоского движения. Плоское движение любого твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости, может быть сведено к движению некоторой неизменяемой плоской фигуры в ее плоскости, складывающемуся из поступательного движения какой-либо точки этой фигуры и вращения ее относительно этой точки. Если в кинематике это может быть любая точка тела, то в динамике удобно пользоваться точкой, в которой находится центр масс тела. Это позволяет применять теорему о движении центра масс и уравнение моментов в его простейшем (обычном) виде.

Вначале проанализируем вопрос о расположении нитей при движении маятника. Поскольку движение происходит под действием силы тяжести и силы натяжения нитей, то устойчивое движение маятника (без раскачивания) возможно только, если нити находятся в вертикальной плоскости (рис. 3).

При отклонении нитей от нее у силы натяжения возникает горизонтальная составляющая, возвращающая маятник к положению, когда нити вертикальны, т. е. возникают колебания, период которых зависит от длины нитей. Это явление наблюдается во время подъема маятника, когда нити выходят из вертикальной плоскости. Перед отпусканием маятника в правильном исходном положении нити должны находиться в вертикальной плоскости, поэтому движение вниз происходит без колебаний (заметим, что при этом центр масс маятника находится не под точкой подвеса нитей!).

Итак, без учета сил трения о воздух и отклонения нитей от вертикали при движении вверх (оно невелико) уравнения движения маятника Максвелла вниз и вверх одинаковы и имеют вид

(1)

(2)

(3)

где m — масса маятника, J — момент инерции маятника относительно его оси, r — радиус стержня маятника, Т — сила натяжения одной нити, g — ускорение силы тяжести, а — ускорение поступательного движения центра масс маятника, e — угловое ускорение маятника. Хотя эти уравнения применимы как к первой, так и к третьей стадии движения маятника, начальные условия для них на разных стадиях различны. При опускании маятника начальная скорость его центра масс равна нулю, при его подъеме она отлична от нуля. Эти уравнения дают

(4)

Поскольку момент инерции маятника можно представить в виде где R — радиус диска, безразмерный коэффициент , величина (радиус диска R много больше радиуса стержня r) и ускорение маятника a<<g, а сила натяжения нитей

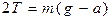(5)

близка к весу маятника mg. Так как при равноускоренном движении (I стадия)

(6)

где t₁ — время опускания маятника, h₁ — расстояние, которое он проходит за это время, то для экспериментального определения момента инерции маятника из (4) и (6) получаем формулу

(7)

Для скорости опускания центра масс маятника непосредственно перед его ударом имеем

(8)

После удара при подъеме маятника вверх (III стадия) он движется равнозамедленно с ускорением а, направленным так же, как при его опускании вниз. Скорость движения центра масс маятника при подъеме определяется уравнением

(9)

где v₂ — начальная скорость движения маятника вверх, t — время от начала этого движения. Появление этой скорости обусловлено продолжающимся по инерции вращением маятника в нижней точке его траектории. Наматывание при этом вращении нитей на стержень маятника и приводит к его подъему.

Если время подъема маятника до его остановки равно t₂, то для величины начальной скорости имеем

(10)

так как величина ускорения при подъеме маятника связана с расстоянием h₂, которое проходит его ось до остановки, таким же соотношением, как и при спуске:

(11)

Величины ускорений при спуске и подъеме должны быть одинаковы. Расстояние h₂, которое проходит ось маятника при его подъеме, несколько меньше, чем при спуске (h₁). Разность этих высот характеризует убыль механической энергии маятника за один цикл его движения: . Убыль энергии связана, вообще говоря, как с неупругими процессами в нитях в момент удара, так и с потерями на трение при движении маятника. Поскольку трение о воздух мало, можно считать, что энергия теряется в момент удара, и ее потеря равна убыли кинетической энергии маятника:

Кинетическая энергия маятника равна

(12)

где — угловая скорость маятника. Поскольку , кинетическая энергия mv²/2, связанная с поступательным движением, мала по сравнению с энергией вращательного движения . Это является главным отличительным признаком маятника Максвелла.

Характерной особенностью маятника Максвелла является малая потеря энергии при ударе: , т. е. близкий к единице коэффициент восстановления скорости . Именно благодаря этому в данной системе можно наблюдать колебания, т. е. многократное повторение цикла движения вниз-вверх, а сама система называется «маятником».

Теперь рассмотрим удар в нижней точке движения маятника. Явление удара сопровождается, как уже упоминалось, резкими изменениями сил взаимодействия при очень малом времени этих изменений. Эти силы сначала нарастают, а затем убывают. Зависимость их от времени, как правило, неизвестна, и применение уравнений движения в явном виде становится невозможным.

В теории удара пользуются выражением для суммарного импульса силы

(13)

где m— масса ударяющегося тела, v₁и v₂ — его скорости до и после удара, F(t) —сила, действующая на тело во время удара, Dt — длительность удара.

В нашем случае во время удара происходит резкое увеличение силы натяжения нитей 2Т. График изменения этой силы приведен на рис. 2, в. Поскольку скорость маятника при ударе меняет свое направление, изменение импульса равно m(v_l+v₂), оно происходит в результате воздействия на маятник импульса силы . Так как при движении маятника вниз и вверх (I и III стадии) сила натяжения нитей мало отличается от веса маятника: (ускорение ), можно считать, что . Таким образом, импульс силы, действующей на маятник при ударе

(14)

т. е. определяется площадью, ограниченной кривой АВСА на рис. 2 в. Поскольку при ударе угловая скорость маятника почти не изменяется (потери энергии малы), можно считать, что во время удара происходит вращение со средней угловой скоростью

(15)

и время удара равно

(16)

Среднее значение силы, исходя из (14) и (16), равно

(17)

Рассмотрим упрощенную картину движения маятника при ударе. Удар начинается в тот момент, когда нити полностью размотались со стержня, а отверстия, в которые они продеты, горизонтальны, и заканчивается через полоборота маятника, в момент начала нового наматывания нитей. Будем считать нити нерастяжимыми, т. е. пренебрежем дополнительным удлинением нитей при ударе dh, возникающим из-за роста сил натяжения, по сравнению с радиусом стержня маятника r:

(18)

При наших предположениях центр масс маятника во время удара совершает движение вниз-вверх по закону (h₀ — вертикальная координата центра масс в начале удара, время отсчитывается от момента начала удара). Поэтому сила, действующая на маятник во время удара,

(19)

(20)

т. е. максимальное увеличение силы натяжения нитей во время удара в p/2 раз превышает среднее значение силы.

Заметим, что поскольку радиус стержня маятника мал по сравнению с длиной нитей h, нити маятника за время удара лишь незначительно отклоняются от вертикальной плоскости: , и небольшая горизонтальная проекция силы натяжения 2T не успевает вызвать заметного смещения центра масс маятника по горизонтали за это время (см. рис. 3, где показаны три последовательных положения оси маятника — в начале (а), в середине (б) и в конце (в) удара). Однако отклонение нитей от вертикальной плоскости, возникающее после удара, приводит к появлению небольшого раскачивания оси маятника во время его подъема (III стадия).

Экспериментальная часть

Принадлежности: 1) установка; 2) секундомер; 3) штангенциркуль; 4) угольник.

задача 1. Определение момента инерции маятника Максвелла относительно его оси

Измерения. Перед началом измерений необходимо убедиться, что длины нитей маятника одинаковы.

Намотав нити на стержень, устанавливают маятник в наивысшем положении. Записав показания секундомера время опускания маятника t, повторяют измерения.

Расстояние h, которое проходит маятник, отсчитывается по шкале при помощи угольника следующим образом. Вначале, удерживая маятник рукой, отмечают угольником на шкале то положение нижнего края сменного кольца, при котором включается секундомер, а затем, размотав нити, отмечают угольником положение верхнего края кольца, соответствующее выключению секундомера. Измерив при помощи штангенциркуля внешний диаметр кольца, добавляют его к полученной разности отсчетов по шкале. Измерения t и h повторяют по 8—10 раз. Затем рассчитывают средние значения и стандартные отклонения t и h (оформление таблицы смотри ниже).

По формуле (6) находят величины ускорений а для всех значений момента инерции маятника, затем по формуле (7) — сами моменты инерции; рассчитывают ошибки найденных величин. Масса маятника, входящая в формулу (7), определяется как сумма масс его частей; эти массы указаны непосредственно на этих частях с точностью до 0,01 г. Радиус r, необходимый для расчета, определяется при помощи штангенциркуля.

Затем, измерив штангенциркулем размеры диска маятника и съемных колец, следует рассчитывать теоретические значения моментов инерции и сравнить их в пределах ошибок с измеренными экспериментально.

Момент инерции однородного диска и цилиндра относительно оси, проходящей через ось симметрии цилиндра можно определить также по формуле:

, (21)

где m₁ - масса цилиндрического тела, R₁ - его радиус.

Используя формулу (21) можно легко получить формулу для моментов инерции полых цилиндрических тел

, (22)

где R₂ - внешний, R₁ - внутренний радиус полого цилиндра.

Момент инерции нескольких тел равен сумме моментов инерции каждого тела в отдельности. Следовательно, момент инерции маятника Максвелла J_P равен сумме моментов инерции диска J_D, кольца J_K и оси J_O:

J_P = J_O + J_D +J_K.

Тогда для момента инерции маятника Максвелла можно получить расчетную формулу:

, (23)

где m_О - масса оси, m_D - масса диска, m_K - масса кольца, R_D - радиус диска, R_K - внешний радиус кольца, R_O - радиус оси.

Заметим, что в данном случае надо пользоваться непосредственно измеренным радиусом стержня, а не его уточненным кинематическим значением, входящим в формулу (7). При анализе ошибок измерений следует пренебречь малыми ошибками.

задача 2. Проверка закона сохранения механической энергии

Маятник, поднятый на высоту 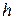, обладает потенциальной энергией . При скатывании маятник одновременно движется поступательно и вращается относительно оси, поэтому его кинетическая энергия

(24)

При падении маятника происходит изменение его потенциальной и кинетической энергии так, что полная механическая энергия остается постоянной согласно закону сохранения механической энергии:

, (25)