Анализ решаемых задач

Математическая модель является хорошим средством получения ответов на широкий круг самых разнообразных вопросов, возникающих при принятии оптимальных решений. Например, на этапе постановки задачи часто производится анализ с целью ответа на вопросы: “что будет, если...?“ и/или “что надо, чтобы...?”. Анализ с целью ответа на первый вопрос называется вариантным анализом; на второй - решениями по заказу. Для задач распределения ресурсов большой интерес представляет решение задачи минимизации используемых ресурсов при заданном результате.

Рассмотрим следующую исходную задачу:

Первая постановка:

F(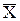)= 4 X1 + 3 X2 + 6 X3 + 7 X4 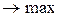(прибыль)

при ограничениях на ресурсы

2 X1 + X2 + X3 + X4 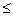280 - (трудовые)

X1 + X3 + X4 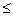80 - (сырье)

X1 + 2 X2 + X3 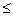250 - (финансы)

Xj 0, j=1,...,4.

Решив задачу получим: 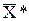= (0, 125, 0, 80), где

X1 = 0 - объем производства продукции вида 1,

X2 = 125 - объем производства продукции вида 2,

X3 = 0 - объем производства продукции вида 3,

X4 = 80 - объем производства продукции вида 4.

F(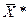) = 935 - прибыль от реализации продукции.

Вторая постановка:

F(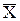)= 4 X1 + 3 X2 + 6 X3 + 7 X4 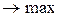(прибыль)

при ограничениях на ресурсы

2 X1 + X2 + X3 + X4 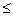280 - (трудовые)

X1 + X3 + X4 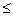80 - (сырье)

X1 + 2 X2 + X3 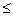250 - (финансы)

X1 10, X2 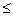100, - (дополнительные

X3 25, ограничения на

X4 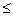50 выпуск продукции)

Xj 0, j=1,...,4.

В результате решения получим: 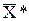= (10, 100, 25, 45), F(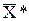) = 805.

Третья постановка:

F(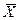) = Y1 + Y2 + Y3 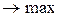(минимизация используемого ресурса)

2 X1 + X2 + X3 + X4 + Y1 = 280 - (трудовые)

X1 + X3 + X4 + Y2 = 80 - (сырье)

X1 + 2 X2 + X3 + Y3 = 250 - (финансы)

X1 10, X2 20 - (задаваемый

X3 25, X4 40. результат)

Y1, Y2, Y3 0 - (неиспользованный ресурс).

Решив задачу получим: 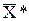= (10, 20, 25, 40), = (175, 5, 175).

При решении по заказу пользователь задает значения тех величин, которые он хочет иметь в оптимальном решении. Такие задачи могут быть трех видов:

1) назначение величины целевой функции;

2) назначение величин искомых переменных;

3) назначение величин используемых ресурсов.

Следует иметь в виду, что во всех этих случаях возможно появление несовместного решения. Рассмотрим такую ситуацию на нашем примере.

Четвертая постановка:

F(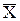)= 4 X1 + 3 X2 + 6 X3 + 7 X4 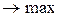(прибыль)

при ограничениях на ресурсы

2 X1 + X2 + X3 + X4 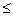280 - (трудовые)

X1 + X3 + X4 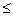80 - (сырье)

X1 + 2 X2 + X3 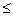250 - (финансы)

X1 100, X2 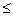100, - (дополнительные

X3 = 30, X4 = 70 ограничения на выпуск продукции)

Xj 0, j=1,...,4.

Очевидно, что для выпуска такого количества продукции располагаемых ресурсов будет недостаточно. Найдем минимальные значения дополнительных необходимых ресурсов каждого вида позволяющих удовлетворить ограничениям задачи.

Пятая постановка:

F(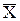) = t1 + t2 + t3 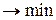(минимизация необходимого дополнительного ресурса)

2 X1 + X2 + X3 + X4 - t1 = 280 - (трудовые)

X1 + X3 + X4 - t2 = 80 - (сырье)

X1 + 2 X2 + X3 - t3 = 250 - (финансы)

X1 100, X2 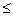100, - (задаваемый результат)

X3 = 30, X4 = 70.

t1, t2, t3 0 - (дополнительный ресурс).

Решив задачу получим: 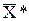= (100, 60, 30, 70), = (80, 120, 0).

Не нашли, что искали? Воспользуйтесь поиском: