
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задачи дробно-линейного программирования
Общая задача дробно-линейного программирования состоит в определении экстремального значения функции
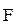 =
= 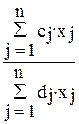 =
= 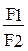 (2.1)
(2.1)
при условиях
 , i = 1,..., m, (2.2)
, i = 1,..., m, (2.2)
xj 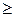 0, j=1,...,n, (2.3)
0, j=1,...,n, (2.3)
где cj, dj, bi и aij - некоторые числа, причем 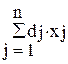 > 0 в области допустимых решений. Такое условие не нарушает общности задачи, поскольку в том случае когда эта величина отрицательна, знак минус можно отнести к числителю. Как и в случае основной задачи линейного программирования, экстремальное значение целевая функция (2.1) принимает в одной из вершин допустимого многогранника (естественно, при условии, что эта задача имеет оптимальный план).
> 0 в области допустимых решений. Такое условие не нарушает общности задачи, поскольку в том случае когда эта величина отрицательна, знак минус можно отнести к числителю. Как и в случае основной задачи линейного программирования, экстремальное значение целевая функция (2.1) принимает в одной из вершин допустимого многогранника (естественно, при условии, что эта задача имеет оптимальный план).
Рассмотрим несколько содержательных примеров на составление математической модели.
Пример 1. Для производства n видов изделий предприятие использует m типов взаимозаменяемого оборудования. Каждый из видов изделий необходимо изготовить в количестве bj единиц (j=1,..,n), причем каждый из типов оборудования может быть занят изготовлением этих изделий не больше чем ai часов (i=1,...,m). Время изготовления одного изделия j-го вида на i-м типе оборудования равно aij часам, а затраты, связанные с производством одного изделия на данном типе оборудования равны cij рублей. Определить сколько изделий каждого вида на каждом из типов оборудования следует произвести так, чтобы себестоимость одного изделия была минимальной.
Пусть Xij - количество изделий j-го вида, изготовляемых на оборудовании i-го типа. Тогда получим
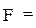

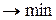 (себестоимость одного изделия)
(себестоимость одного изделия)
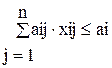 (i=1,..., m) – (ограничения на время),
(i=1,..., m) – (ограничения на время),
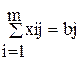 (j = 1,..., n) – (ограничения на выпуск изделий),
(j = 1,..., n) – (ограничения на выпуск изделий),
Xij 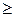 0, (i=1,...,m), (j=1,...,n) - (условия неотрицательности).
0, (i=1,...,m), (j=1,...,n) - (условия неотрицательности).
Пример 2. Для выполнения n различных работ могут быть использованы рабочие m квалификационных групп. При выполнении j-й работы i-й группой рабочих выработка в единицу времени равна cij (i=1,...,m), (j=1,...,n) рублей. Общий фонд времени, в течение которого i-я группа рабочих может быть занята выполнением работ, не превышает bi единиц времени, а объем j-й работы равен aj рублей. Составить такой план выполнения работ, при котором производительность труда является максимальной.
Пусть Xij - время, выделяемое рабочими i-й квалификационной группы на j-ю работу. Тогда
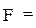
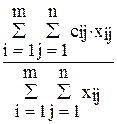
 – (производительность труда),
– (производительность труда),
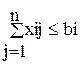 (i=1,...,m) - (ограничения на время),
(i=1,...,m) - (ограничения на время),
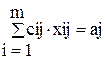 (j=1,...,n) – (ограничения на объем работы),
(j=1,...,n) – (ограничения на объем работы),
Xij 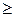 0, (i = 1,..., m), (j = 1,..., n) – (условия неотрицательности).
0, (i = 1,..., m), (j = 1,..., n) – (условия неотрицательности).
Сформулированная выше задача (2.1)-(2.3) может быть сведена к задаче линейного программирования. Для этого следует обозначить
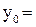
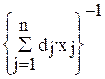 (2.4)
(2.4)
и ввести новые переменные 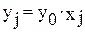 , (j = 1,..., n). (2.5)
, (j = 1,..., n). (2.5)
Тогда исходную задачу (2.1)-(2.3) можно записать в виде
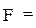
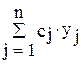 (2.6)
(2.6)
при условиях
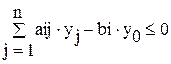 , (i=1,...,m), (2.7)
, (i=1,...,m), (2.7)
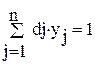 (2.8)
(2.8)
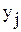
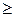 0, (j=1,...,n),
0, (j=1,...,n), 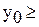 0.
0.
Задача (2.6) - (2.8) является задачей линейного программирования и, следовательно, ее решение можно найти известными методами. Зная оптимальный план этой задачи, на основе соотношений (2.5) получим оптимальный план исходной задачи (2.1) - (2.3).
Пример 3.
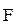 =
= 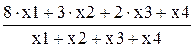

2 * X1 + X2 + X3 + 3 * X4 £ 300
X1 + 2 * X3 + X4 £ 70
X1 + 2 * X2 + X 3 £ 340
Xj 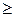 0, (j = 1,..., 4).
0, (j = 1,..., 4).
Сведем данную задачу к задаче линейного программирования. Для этого обозначим  через
через 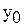 и введем новые переменные
и введем новые переменные
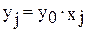 , (j=1,...,4). В результате приходим к следующей задаче:
, (j=1,...,4). В результате приходим к следующей задаче:
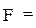 8 * Y1 + 3
8 * Y1 + 3  Y2 + 2 * Y3 + Y4
Y2 + 2 * Y3 + Y4 
2 * Y1 + Y2 + y3 + 3 * Y4 - 300 * Y0 £ 0
Y1 + 2 * Y3 + Y4 - 70 * Y0 £ 0
Y1 + 2 * Y2 + y3 - 340 * Y0 £ 0
Y1 + Y2 + Y3 + Y4 = 1
Y0, Yj 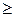 0, (j=1,...,4).
0, (j=1,...,4).
Решив данную задачу получим:
 (Y0, Y1, Y2, Y3, Y4) = (1/70, 1, 0, 0, 0)
(Y0, Y1, Y2, Y3, Y4) = (1/70, 1, 0, 0, 0)
Используя соотношения 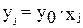 , определяем оптимальный план исходной задачи
, определяем оптимальный план исходной задачи
 (X1, X2, X3, X4) = (70, 0, 0, 0), F(
(X1, X2, X3, X4) = (70, 0, 0, 0), F(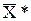 ) = 8.
) = 8.
Не нашли, что искали? Воспользуйтесь поиском: