Задачи целочисленного программирования

Значительная часть задач производственного менеджмента, относящихся к задачам линейного программирования, требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции.

Целочисленное программирование ориентировано на решение задач, в которых все или некоторые переменные должны принимать только целые значения. Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные; когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной.

Математическая модель линейной целочисленной задачи может быть записана следующим образом:

F(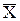) = (1)

, bi 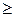0, i = 1,..., m, (2)

xj 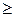0, j = 1,..., n, xj – целые. (3)

Существует эвристический подход к решению задач целочисленного программирования (ЗЦП), основанный на решении ЗЦП как задачи ЛП. Использование процедур округления нецелочисленного оптимального решения задачи ЛП дает возможность получать приближенное оптимальное целочисленное решение. Например, если в оптимальном решении двумерной задачи ЛП значения переменных х1 и х2 оказались равными 3,5 и 4,4 соответственно, то в качестве кандидатов на роль приближенного целочисленного оптимального решения необходимо рассмотреть точки (3;4), (4;4), (4;5), (3;5) полученные в результате округления. Заметим однако, что истинное оптимальное целочисленное решение может не совпадать ни с одним из четырех, указанных выше.

ПРИМЕР

F(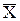) = x1 – 3×x2 + 3×х3

при ограничениях

2×x1 + x2 - х3 £ 4

4×x1 - 3×x2 £ 2

-3×x1 + 2×x2 + х3 £ 3

x1, х2, х3 ³ 0, целые.

Игнорируя условия целочисленности получим . Никакое округление компонент этого плана не дает допустимого решения, так как искомое целочисленное решение . Таким образом, для решения целочисленных задач необходимы специальные методы.

Точные методы решения задач целочисленного программирования можно классифицировать как методы отсечений и комбинаторные методы.

Название “методы отсечений” связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами. Метод отсекающих плоскостей, разработанный Р. Гомори, используется при решении полностью целочисленных задач.

В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений. Разумеется, на первый план здесь выдвигается проблема разработки процедур, позволяющих непосредственно рассматривать лишь относительно небольшую часть указанных решений, а остальные допустимые решения учитывать некоторым косвенным образом. Наиболее известным комбинаторным методом является метод ветвей и границ.

Не нашли, что искали? Воспользуйтесь поиском: