Абсолютная энтропия

В отличие от многих других термодинамических функций, энтропия имеет точку отсчета, которая задается постулатом Планка (третьим законом термодинамики): при абсолютном нуле (T = 0) К все идеальные кристаллы имеют одинаковую энтропию, равную нулю.

При стремлении температуры к абсолютному нулю не только энтропия стремится к 0, но и ее производные по всем термодинамическим параметрам:

(x = P, V).

Это означает, что вблизи абсолютного нуля все термодинамические процессы протекают без изменения энтропии. Это утверждение называют тепловой теоремой Нернста.

Постулат Планка позволяет ввести понятие абсолютной энтропии вещества, т.е. энтропии, отсчитанной от нулевого значения при T = 0. Для расчета абсолютной энтропии веществ в стандартном состоянии надо знать зависимости теплоемкости от температуры для каждой из фаз, а также температуры и энтальпии фазовых переходов. Так, например, абсолютная энтропия газообразного вещества в стандартном состоянии при температуре T складывается из следующих составляющих:

В термодинамических таблицах обычно приводят значения абсолютной энтропии в стандартном состоянии при температуре 298 К ().

Значения абсолютной энтропии веществ используют для расчета изменения энтропии в химических реакциях:

(2.14)

Пример 2.1.

В двух сообщающихся сосудах, разделенных перегородкой, находятся 1 моль азота и 2 моль кислорода. Перегородку вынимают, газы смешиваются. Рассчитать изменение энтропии (Δ S _смеш), если исходные температуры и давления одинаковы, а объемы различны; 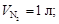Конечное давление смеси равно исходному давлению газа.

Процесс смешения газов необратим, и изменение энтропии выражается неравенством Δ S > . Но если необратимый и обратимый процессы проводятся в одних и тех же граничных условиях, то Δ S _обр = Δ S _необр. Всякий необратимый процесс можно мысленно провести обратимо в несколько стадий в тех же граничных условиях и подсчитать энтропию для каждой обратимой стадии. Тогда сумма изменений энтропии этих стадий будет равна изменению энтропии необратимого процесса. В данной задаче общее изменение энтропии можно заменить суммой изменения энтропий за счет расширения каждого из газов по отдельности, т.е. принять, что Δ S _смеш =

Согласно уравнению (2.13)

Молярные доли азота и кислорода следующие:

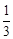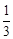Δ S _смеш = – 3×8,314( ln + ln ) = 15,876 Дж/(моль·К)

Пример 2.2.

Определить изменение энтропии при смешении 1 кмоль аргона, взятого при температуре 293 К (Т _Ar)
c 2 кмоль азота, находящимися при температуре 323 К (). Исходные давления компонентов и конечное давление смеси одинаковы. Принять аргон и азот идеальными газами, а теплоемкость каждого газа – величиной, постоянной в указанном интервале температур и равной:

для азота C_V = 20,935∙10³ Дж/(кмоль·К),

для аргона C_V = 12,561∙10³ Дж/(моль·К).

Решение.

Изменение энтропии (Δ S) в этом процессе равно изменению энтропии аргона и энтропии азота:

Δ S = Δ S _Ar +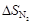

Для решения задачи необходимо найти температуру смеси по уравнению

где – исходные давления газов; , – парциальные давления компонентов после смешения газов.

Парциальное давление каждого газа определяем по закону Дальтона:

Изменение энтропии аргона и азота:

Изменение энтропии в процессе смешения:

Пример 2.3.

Газообразные водород и хлор при 25 °С поступают в реактор синтеза хлороводорода, где взаимодействуют при 725 °С по реакции

Cl_2(г) + H_2(г) = 2HCl_(г).

Определить изменение энтропии системы, начиная с момента поступления газов в реактор, если их объемный расход одинаков.

Решение.

Процесс состоит из трех стадий: смешение исходных веществ, нагревание их до температуры 725 °С и химическое превращение. В соответствии с этим, изменение энтропии системы включает следующие энтропии:

смешения – Δ S _смеш;

изобарического нагревания компонентов и

химического превращения Δ S _х.р.

Проведем расчет на один пробег реакции.

Исходная смесь состоит из 1 моль H_2(г) и 1 моль Cl_2(г), следовательно, молярные доли компонентов перед началом реакции одинаковы: x ₁= x ₂ = 0,50. Отсюда имеем

Дж/(К·проб).

Определяем изменение энтропии при изобарном нагревании компонентов системы по отдельности:

для H_2(г)

Дж/(К·проб);

для Cl_2(г)

Дж/(К·проб);

где 29,57 и 36,50 – значения изобарных теплоемкостей водорода и хлора, в Дж(моль·К), средние в температурном интервале 25–725 °С (298–998 К).

Изменение энтропии системы на стадии химического превращения определяем по закону Гесса, значения стандартных энтропий участников реакции берем из приложения 12:

для водорода = 130,52 Дж/(моль·К);

для хлора = 222,98 Дж/(моль·К);

для хлороводорода = 186,79 Дж/(моль·К).

Исходя из следствия из закона Гесса, имеем

Δ S _х.р = 2∙186,79 – (130,52 + 222,98) = 20,08 Дж/(К·проб).

Суммируя результаты расчетов для всех стадий процесса, получаем

Пример 2.4

Рассчитать изменение энтропии при нагревании 0,7 моль моноклинной серы от 25 до 200 °С при давлении 1 атм. Мольная теплоемкость серы

C_P (S _(т)) = 23,64 Дж/(моль·К),

C_P (S _(ж)) = 35,73 + 1,17×10^–3 T Дж/(моль·К).

Температура плавления моноклинной серы 119 °С, удельная теплота плавления 45,2 Дж/г.

Решение.

Общее изменение энтропии складывается из трех составляющих: 1) нагревание твердой серы от 25 до 119 °С; 2) плавление; 3) нагревание жидкой серы от 119 до 200 °С.

Дж/К.

Дж/К.

D S = D S ₁ + D S ₂ + D S ₃ = 11,88 Дж/К.

Пример 2.5.

Рассчитать изменение энтропии 1000 г воды в результате ее замерзания при –5 °С. Теплота плавления льда при 0 °С равна 6008 Дж/моль. Теплоемкости льда и воды соответственно равны 34,7 и 75,3 Дж/(моль·К). Объяснить, почему энтропия при замерзании уменьшается, хотя процесс замерзания идет самопроизвольно.

Решение.

Необратимый процесс замерзания воды при –5 °С можно представить в виде последовательности обратимых процессов: 1) нагревание воды от –5 °С до температуры замерзания 0 °С; 2) замерзание воды при 0 °С; 3) охлаждение льда от 0 до –5 °С.

Изменение энтропии в первом и третьем процессах (при изменении температуры) рассчитывается по формуле (2.9):

Изменение энтропии во втором процессе рассчитывается как для обычного фазового перехода (2.12). Необходимо только иметь в виду, что теплота при замерзании выделяется:

.

Так как энтропия – функция состояния системы, то общее изменение энтропии равно сумме изменений энтропии в этих трех процессах:

Δ S = Δ S ₁ + Δ S ₂ + Δ S ₃ = –1181 Дж/К.

Энтропия при замерзании убывает, хотя процесс самопроизвольный. Это связано с тем, что в окружающую среду выделяется теплота, и энтропия окружающей среды увеличивается, причем это увеличение больше, чем 1181 Дж/К, поэтому энтропия Вселенной при замерзании воды возрастает, как и полагается в необратимом процессе.

Пример 2.6

Определить изменение энтропии для реакции

Cd + 2AgCl = CdCl₂ + 2Ag.

Если проводить ее в гальваническом элементе при давлении 101 325 Па и температуре 298 К, ЭДС элемента компенсируется приложенной извне и равной 0,6753 В. Стандартные теплоты образования хлоридов кадмия и серебра соответственно равны –389,0 и –126,8 кДж/моль.

Решение.

Тепловой эффект реакции в соответствии с законом Гесса

= –38900 – 2(– 126800) = –135400 Дж.

Так как реакция необратима, то > – .

Для расчета Δ S _х.рнеобходимо реакцию провести обратимо. Если же осуществлять эту реакцию в помещенном в термостат гальваническом элементе, в котором поддерживаются неизменными температура и давление, и если ЭДС элемента Е компенсируется ЭДС, приложенной извне, то процесс будет практически обратимым. При этом будет произведена работа

W _max = nFE,

а тепловой эффект Q будет равен Т Δ S:

Δ U = Q – W _max = Q – (P Δ V + W' _max),

или Q = Δ H + W' _max = Δ H + nFE.

Подставляя в последнее уравнение значения (изменение энтальпии не зависит от пути процесса, поэтому оно будет одинаковым как в необратимом, так и в обратимом процессах) и n = 2, Е = 0,6753 В и F = 96 487 Кл, получаем

Q = – 135 400 + 2∙0,6753∙96 487 = –5084,7 Дж.

Следовательно, Дж/(моль·К). Изменение энтропии изолированной системы в целом (т.е. рабочая система плюс термостат) при фактическом процессе

Δ S _{изол. сист} = – 17,05 + Дж/(моль·К),

что подтверждает необратимость процесса.

Пример 2.7.

Установить, осуществима ли при V = const и 298 К реакция

Ag_(т) + n Cl_2(г) = AgCl_(т) + (n – 0,5)Cl_2(г),

используя свойства энтропии.

Решение.

Энтропия является критерием направленности процесса только в том случае, если процесс протекает в изолированной системе, поэтому мысленно проводим исследуемую реакцию при V = const и отсутствии теплообмена с окружающей средой. Чтобы рассчитать Δ S процесса, принимаем:

1) реакция проходит мгновенно и до конца при температуре 298 К;

2) выделившаяся теплота идет на нагревание избытка газообразного хлора и твердого хлорида серебра;

3) реакционный сосуд теплоту не поглощает.

Тогда общее изменение энтропии складывается из энтропии реакции (Δ S _х.р) и энтропии нагревания хлора и хлорида серебра (Δ S _нагр):

Δ S = Δ S _х.р + Δ S _нагр.

Вычислим

Значения стандартных энтропий выписываем из приложения 12:

После подстановки чисел и вычислений получаем

Для вычисления Δ S _нагр сначала по уравнению теплового баланса определяем конечную температуру газообразного хлора и твердого хлорида серебра. Составляем уравнение теплового баланса, предположив, что конечная температура системы выше температуры плавления хлорида серебра:

Принимаем, что избыток Cl_2(г) составляет Справочные данные, необходимые для расчета, находим в приложении 12.

Дж/(моль·К); Дж/моль;

Определяем теплоемкость при постоянном объеме:

Дж/(моль·К).

Вычисляем конечную температуру, а затем рассчитываем изменение энтропии при нагревании:

Дж/(моль·К);

вычисляем по уравнению (2.8) и соотношению :

Рассчитываем интегралы:

Подставляем полученные значения в уравнение для расчета Δ S _нагр.

Δ S _нагр= 81,67 + 5(38,28 – 8,895) = 228,595 Дж/кг.

Отсюда общая энтропия процесса

Δ S = – 57,91 + 228,6 = 170,7 Дж/К.

Таким образом, изменение энтропии положительно (Δ S > 0). Реакция в принятых условиях V = const и Т = 298 К осуществима.

Пример 2.8.

Определить изменение энтальпии, внутренней энергии и энтропии при переходе 2,7 кг воды, взятой при
Р ₁= 101 325 Па и Т ₁ = 293 К, в пар при Р ₂ = 50 665 Па
и Т ₂ = 373 К. Принять, что С_Р = С_V = 4,187∙10³ Дж/(кг·К). Удельная теплота испарения l = 2260,98∙10³ Дж/кг. Считать пар идеальным газом.

Решение.

Изменение свойств системы не зависит от пути процесса, а определяется только начальным и конечным состояниями системы. Поэтому выберем любой путь, состоящий из отдельных обратимых стадий, и тогда изменение свойства в данном процессе будет равно сумме изменений свойства в каждой стадии.

Допустим, что процесс состоит из обратимых стадий:

1) нагрев воды при Р ₁ = 101325 Па от Т ₁ = 293 Кдо
Т ₂ = 373 К;

2) превращение воды в пар при Р ₁= 101 325 Па
и Т ₂ = 373 К;

3) изотермическое расширение водяного пара при
Т ₂ = 373 Кот Р ₁ = 101 325 Па до Р ₂ = 50 665 Па:

Δ Н = Δ Н ₁ + Δ Н ₂ + Δ Н ₃;

Δ Н ₃ = 0,

так как, согласно закону Джоуля, энтальпия и внутренняя энергия идеального газа при постоянной температуре не зависят от давления или объема.

Следовательно,

Δ Н = 904,392 ∙10³ + 6104,616 ∙10³ = 7009,038 ∙10³ Дж.

Δ U = Δ U ₁ + Δ U ₂ + Δ U ₃, так как С_Р = С_V,

Δ U ₁ = Δ Н ₁ = 904,392∙10³ Дж,

Δ U ₂ = Δ Н ₂ – Р Δ V = Δ Н ₂ – Р (V_п – V _ж), объемом жидкой фазы пренебрегаем.

Δ U ₂ = Δ Н ₂ – РV_п = Δ Н ₂ – nRT ₂ .

Δ U ₂ = 6104,646∙10³ –

Δ U ₃ = 0;

Δ U = 904,392 ∙10³ + 5639,419 ∙10³ = 6543,811 ∙10³ Дж.

Δ S = Δ S ₁ + Δ S ₂ + Δ S _3,

Δ S = 3,525 ∙10³ + 16,366 ∙10³ + 0,865 ∙10³ = 20,756 ∙10³ Дж/К.

Не нашли, что искали? Воспользуйтесь поиском: