Для об’єкта, модель якого шукається у вигляді

, (16)

алгоритм знаходження параметрів v_і, 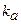і Т подібний до наведеного в пункті д). Різниця полягає в тому, що спочатку з кривої розгону об’єкта регулювання визначають час запізнення, і пряму паралельну до асимптоти проводять через точку t=t. Теоретична крива розгону для моделі (16) описується рівнянням

. (17)

1.1.3. Інженерні методи побудови моделей за експериментальними імпульсними перехідними характеристиками.

Зняття кривої розгону об’єкта регулювання пов’язане з тривалим відхиленням технологічного параметру від номінального значення. Це може привести до погіршення якісних та економічних показників технологічного процесу в цілому. В такому разі більш доцільним є метод імпульсної перехідної характеристики [8,9].

Під дією імпульсної зміни вхідної величини відхилення регульованої величини від номінального є менш тривалими. При знятті імпульсної перехідної характеристики значення імпульсної зміни вхідної величини може бути значно більшим за значення стрибкоподібної зміни, що може сприяти підвищенню точності знаходження математичної моделі.

Типові імпульсні перехідні функції об’єктів регулювання із самовирівнюванням та без самовирівнювання показані на рис. 4a, 4б.

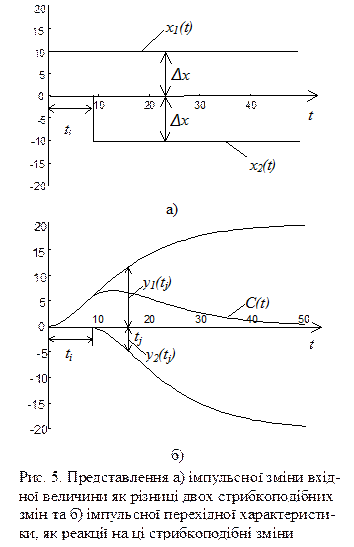
Імпульсну зміну вхідної величини можна розглядати як алгебраїчну суму двох однакових за величиною стрибкоподібних змін і , зсунутих на час тривалості імпульсу t_i, і спрямованих в протилежні сторони рис. 5а. Відповідно і імпульсна перехідна характеристика є реакцією на них і являє собою суму двох кривих розгону . Як видно з рис. 5б, на відрізку тривалості імпульсу від 0 до t_i імпульсна перехідна характеристика збігається з кривою розгону , а для моментів часу t_j › t_i її значення визначаються за формулою

.

З останнього рівняння також видно, як можна побудувати криву розгону за відомою імпульсною перехідною характеристикою. Для цього необхідно, в кожний моменту часу t_j> t_i до значень імпульсної перехідної характеристики додавати значення кривої розгону, в моменти часу, зсунуті на тривалість імпульсу t_i назад, тобто .

Методика такої побудови ілюструється рисунком 6. Таким чином з експериментальної імпульсної перехідної характеристики можна за наведеною вище методикою одержати криву розгону, а для побудови моделі - застосувати розглянуті вище методи.

Коефіцієнт передачі об’єкта із самовирівнюванням з експериментальної імпульсної перехідної характеристики визначають з формули

, (18)

де - площа під експериментальною імпульсною перехідною характеристикою; - площа під імпульсної зміною вхідної величини. Очевидно, що розмірністю коефіцієнта передачі є відношення розмірності вихідної величини до розмірності вхідної. Для об’єкта без самовирівнювання швидкість розгону з експериментальної імпульсної перехідної характеристики визначають з відношення

, (19)

де -усталене відхилення регульованої величини від номінального, викликане імпульсною зміною вхідної величини.

1.1.4. Чисельні методи знаходження параметрів моделі заданої структури

В практиці побудови моделей за експериментальними значеннями кривої розгону (або імпульсної перехідної характеристики) може бути застосований метод найменших квадратів (МНК). Згідно з цим методом за виглядом експериментальної кривої розгону обирають структуру функції передачі , для якої встановлюють криву розгону і формують суму квадратів різниць між теоретичними та експериментальними значеннями кривої розгону у задані моменти часу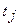

, (20)

де N – кількість експериментальних значень кривої розгону; вектор параметрів заданої функції передачі. Згідно з МНК параметри функції передачі мають бути такими, щоб забезпечити найменше значення суми (20)

.

Таким чином, задача зводиться до пошуку значень параметрів заданої функції передачі, при яких забезпечується мінімальне значення функції . Її можна вирішувати аналітично або чисельним методом. При аналітичному методі по кожному з шуканих параметрів знаходять похідні від функції і прирівнюють їх до нуля. В результаті отримують систему n рівнянь (де n – кількість невідомих параметрів)

, (21)

розв’язок, якої дозволяє знайти значення невідомих параметрів.

Для знаходження похідних необхідно мати аналітичне рівняння кривої розгону для заданої функції передачі. Криві розгону для функцій передачі, що звичайно застосовують для технологічних об’єктів, є нелінійним і трансцендентним. Відповідно часткові похідні описуються також трансцендентними і нелінійними рівняннями. Аналітичний розв’язок системи таких рівнянь (21) відносно шуканих параметрів є складним, а то й неможливим. Тому таку задачу зручніше розв’язувати чисельним методом.

При чисельному методі знаходження параметрів моделі зручно скористатись пакетом Мatlab, в якому є програми, що дозволяють створювати функції передачі різної структури, знаходити їх перехідні функції, вирішувати оптимізаційні задачі. Параметри вибраної моделі можна знайти, застосовуючи функцію fminsearch. Приклад знаходження параметрів функції передачі заданої структури наведений в додатку 2. Головна програма записана у script -файлі використовує функцію suma, в якій описано функцію s= суму квадратів відхилення між експериментальними та розрахунковими значеннями перехідних функцій. В основній програмі викликається функція fminsearch, яка знаходить такі значення параметрів моделі, при яких забезпечується мінімум функції suma. Пошук параметрів моделі здійснюється ітераційно за алгоритмом Нелдера-Міда. Знайдені за допомогою fminsearch параметри, записані в змінну х, і є шуканими параметрами заданої функції передачі.

Слід відзначити, що коректне застосування функцій Мatlab Step та Impulse можливе, якщо значення експериментальної перехідної функції (або імпульсної перехідної характеристики) задані з постійним кроком часу. Саме для такого випадку побудовані головна програма та функція sumа, наведені в додатку 1. Якщо крок значень експериментального вектора часу змінний, то значення експериментальної перехідної (або імпульсної перехідної характеристики) необхідно знаходити за допомогою їх аналітичних виразів або виразів, що їх апроксимують.

Не нашли, что искали? Воспользуйтесь поиском: