Розширена АФХ ПІ-регулятора записується у вигляді

. (28)

Підставляючи (28) в (27) одержимо

,

або

,

звідки отримуємо систему двох рівнянь з двома невідомими

.

Розв’яжемо отриману систему рівнянь відносно

. (29)

Розширена АФХ об’єкта регулювання в показниковій формі має вигляд ,

де розширені амплітудно- і фазочастотні характеристики об’єкта регулювання. Враховуючи, що дійсна U і уявна V розширені частотні характеристики визначаються як система (29) набуде вигляду

. (30)

Змінюючи частоту в діапазоні ( - частота, що відповідає параметру настроювання І-регулятора; - частота, що відповідає параметру настроювання П-регулятора) розраховують область параметрів настроювання ПІ-регулятора на задану ступінь коливальності m_зад. Аналітично частоти і можна визначити з рівнянь

.

Графічно границя області заданого запасу стійкості представлена на рис. 7.

На цьому ж графіку показана область параметрів настроювання регулятора, що виводять САР на границю стійкості (m = 0). Якщо вважати, що діючі в САР збурення є низькочастотними (зокрема детерміноване збурення у вигляді стрибка є низькочастотним), то оптимальні параметри настроювання розраховують при частоті , при якій . Для випадкових збурень вибирають параметри настроювання з границі області запасу стійкості на робочій частоті . Вважається, що таким чином визначені параметри, наближено забезпечують мінімальне значення інтегральної квадратичної оцінки якості J₂

(31)

де - крива розгону замкнутої САР; - задане значення регульованої величини.

Для точного визначення оптимальних параметрів настроювання регулятора необхідно розрахувати значення J₂ за рівнянням (31) при різних значеннях параметрів настроювання регулятора зі знайденої області заданого запасу стійкості. і знайти таку пару значень , при якій J₂ набуде найменшого значення. Таким чином, оптимальними параметрами настроювання регулятора є такі, що при заданому запасі стійкості САР забезпечують мінімальне значення інтегральної оцінки якості.

б) Розрахунок параметрів настроювання ПІД-регулятора.

Функція передачі ПІД-регулятора має вигляд

(32)

де, крім зазначених, Т_д – час диференціювання.

В загальному випадку границя заданого запасу стійкості є деякою поверхнею в тривимірному просторі параметрів настроювання . Якщо один з параметрів зафіксувати, то розрахунок зводиться до визначення двох інших параметрів настроювання. Так, якщо задатись часом диференціювання , то значення двох інших параметрів настроювання ПІД-регулятора розраховують за формулами

(33)

Для заданих значень в площині параметрів будується границя області запасу стійкості, з якої визначають оптимальні значення параметрів настроювання . Для деяких типів аналогових регуляторів розраховані оптимальні значення параметрів настроювання ПІД-регулятора повинні задовольняти умові

.

Якщо остання умова не виконується, то необхідно зменшити час диференціювання і повторити розрахунок.

2.2.2 Розрахунок каскадних систем автоматичного регулювання.

Застосування багатоконтурних систем регулювання, зокрема каскадних, має сенс у тому випадку, коли можливості одноконтурних систем вже вичерпані [2,7]. Вони застосовуються, звичайно для об'єктів регулювання з великим запізненням, для об’єктів з розподіленими параметрами для яких випереджаючу інформацію про вплив на значення регульованої величини можна отримати з проміжної точки, що має менше запізнення і швидше сприймає збурення. Такі системи дозволяють підвищити якість процесів регулювання: зменшити час регулювання, максимальне динамічне відхилення тощо.

Таким чином, каскадні системи регулювання застосовують для об’єктів регулювання, що мають велику інерційність каналом регулюючої дії. В таких системах обирають менш інерційну до найбільш небезпечних збурень допоміжну вихідну величину з такою ж регулюючу дію. В каскадній системі регулювання (див. рис. 8) є два регулятори - основний (зовнішній або коректуючий), що підтримує основну вихідну величину y на заданому значенні та допоміжний (внутрішній або стабілізуючий), призначений для регулювання допоміжної вихідної величини y₁ . Вихідний сигнал основного регулятора [2, 14] може бути завданням для допоміжного регулятора або коректувати може його коректувати. Для підтримання основного регульованого параметру на заданому значенні без статичної похибки закон регулювання основного регулятора мусить мати інтегральну складову. Від допоміжного регулятора вимагається в першу чергу швидкодія, тому він може бути і пропорційним.

Розрахунок каскадних САР полягає у визначенні параметрів настроювання основного і допоміжного регуляторів при заданих функціях передачі об'єкта регулювання за основною у і допоміжною y₁ вихідними величинами [1]. Процедура розрахунку такої системи є ітераційною. Кожна ітерація складається з двох кроків. На кожному кроку ітерації розраховують приведену одноконтурну систему, в якій параметри настроювання одного з регуляторів визначають відносно відповідного еквівалентного об'єкта. Як видно із структурної схеми на рис. 9 еквівалентний об'єкт для основного регулятора АР з функцією передачі W_AP(p) є послідовним з'єднанням замкнутого допоміжного контуру і об'єктом регулювання за основною вихідною величиною. Функція передачі такого еквівалентного об'єкта визначається добутком функцій передачі послідовно з'єднаних елементів

(34)

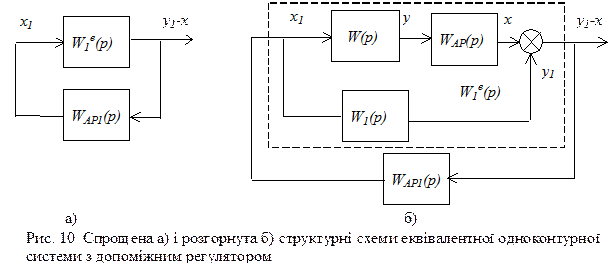
Еквівалентний об'єкт для допоміжного регулятора АР1 (рис. 10) є паралельним з'єднанням об'єкта за допоміжною вихідною величиною і розімкненою системою за основною регульованою величиною. Його функція передачі має вигляд

(35)

Залежно від першого кроку ітерації є два варіанти розрахунку каскадних САР.

Перший варіант застосовують тоді, коли інерційність допоміжного каналу суттєво менша від основного. При цьому розрахунок починають з основного регулятора.

На першому кроку розрахунку припускають, що робоча частота основного контуру набагато менше частоти допоміжного контуру, тому в першому наближенні можна прийняти функцію передачі еквівалентного об'єкта у вигляді

, (36)

де верхній індекс (1) біля функції передачі еквівалентного ОР означає номер ітерації.

Таким чином на першому кроку параметри настроювання основного регулятора залежать від функцій передачі об’єкта регулювання і не залежать від параметрів допоміжного регулятора. Розрахунок параметрів настроювання основного регулятора можна здійснювати одним з відомих методів (методом розширених частотних характеристик, методом незаникаючих коливань Циглера-Нікольса). Простіше застосувати наближений метод розрахунку – метод Циглера-Нікольса [2].

На другому кроку першої ітерації розраховують параметри настроювання допоміжного регулятора АР1 для еквівалентного об’єкта (35) з функцією передачі , куди підставляють функцію передачі основного регулятора з параметрами настроювання, розрахованими на першому кроку.

В наближених розрахунках каскадних систем регулювання обмежуються першими двома кроками. При точних розрахунках здійснюють другу ітерацію, під час якої уточнюють параметри настроювання основного регулятора для еквівалентного об’єкта з функцією передачі за рівнянням (34), куди підставляють значення параметрів настроювання допоміжного регулятора, розраховані в першій ітерації на другому кроку. Далі знов розраховують параметри допоміжного регулятора за функцією передачі еквівалентного об’єкта за формулою (35), в яку підставляють параметри настроювання основного регулятора, розраховані на третьому кроку другої ітерації. Ітерації продовжують доти, доки параметри відповідно основного і допоміжного регуляторів не збігатимуться із заданою точністю. На практиці застосовують дві-три ітерації (4-6 кроків).

За другим варіантом розрахунок починають із допоміжного регулятора, вважаючи, що зовнішній регулятор відключений, тобто

(37)

Таким чином, в першому наближенні розраховують параметри настроювання допоміжного регулятора АР1 за функцією передачі об’єкта регулювання по допоміжному параметру. На другому кроку розраховують параметри настроювання основного регулятора за функцією передачі еквівалентного об’єкта за рівнянням (34) з врахуванням розрахованих на першому кроку параметрів настроювання допоміжного регулятора. В другій ітерації уточнюють параметри настроювання допоміжного регулятора за функцією передачі еквівалентного об’єкта регулювання з рівняння (35), де у функцію передачі основного регулятора підставляють параметри настроювання, розраховані на другому кроку. Як і в першому варіанті, розрахунки проводять доти, доки параметри настроювання регуляторів в двох послідовних ітераціях не збігатимуться із заданою точністю.

2.2.3 Розрахунок комбінованих систем автоматичного регулювання.

Комбіновані САР поєднують принципи регулювання за відхиленням та за збуренням. Вони застосовуються для автоматизації об’єктів, робота яких суттєво залежить від дії збурень. Такі системи регулювання мають два канали дії на регульовану величину: один з них є замкнутим, другий розімкненим [2].

Структурна схема комбінованої САР показана на рис.11.

Метою розрахунку комбінованих систем є отримання інваріантної САР, тобто такої, в якій відхилення вихідної величини від заданого значення під дією збурень тотожно дорівнює нулю. Очевидно, що досягнути абсолютну інваріантність в реальних САР практично неможливо. Звичайно обмежуються частковою інваріантністю по відношенню до найбільш небезпечного збурення. Розглянемо, наприклад, умову інваріантності САР, структурна схема якої зображена на рис. 11б, яка в спрощеному вигляді показана на рис. 12. Застосуємо до цієї схеми структурні перетворення, а саме перенесемо лінію зв’язку з входу автоматичного регулятора на вихід, тоді одержимо схему, показану на рис. 13. Функція передачі блоку елементів І має вигляд

,

а блоку елементів ІІ –

.

Умова інваріантності полягає в тому, що під дією збурення z зміна регульованої величини y має дорівнювати нулю. Згідно з перетвореною структурною схемою вихідний сигнал САР в операторній формі дорівнює

. (38)

З цього виразу видно, що буде тотожно дорівнювати нулю, якщо виконується умова

, (39)

звідки можна знайти теоретичну функцію передачі компенсатора , яка забезпечить інваріантність САР до збурення z

. (40)

Таким чином, функція передачі компенсуючої ланки буде залежати від характеристик об’єкта регулювання каналами дії регулятора і збурення і самого автоматичного регулятора. Функція передачі компенсатора може бути складною, а в деяких випадках навіть такою, що фізично не реалізується. На практиці для побудови комбінованої системи звичайно обирають компенсатор із спрощеною функцією передачі, яку легко реалізувати. При цьому параметри такого компенсатора обирають такими, щоби його частотні характеристики збігалися з частотними характеристиками теоретичного компенсатора на деяких частотах. Характерними частотами є нульова частота, що характеризує САР в усталеному режимі, та робоча частота, при якій досягається максимум амплітудно-частотної характеристики. Тому найчастіше функцію передачі спрощеного компенсатора вибирають такою, щоби амплітудно-фазові характеристики наближеного та теоретичного компенсаторів збігались саме при цих значеннях частот. Звичайно спрощені компенсатори це послідовно з’єднані диференціюючі та аперіодичні ланки. Таким чином, розрахунок інваріантної САР полягає у

- розрахунку параметрів настроювання регулятора замкнутої САР,

- знаходженні теоретичної функції передачі компенсатора за рівнянням (40),

- виборі функції передачі наближеного компенсатора та визначенні його параметрів з умови максимального збігу амплітудно-фазових характеристик наближеного та теоретичного компенсаторів в робочому діапазоні частот.

Не нашли, что искали? Воспользуйтесь поиском: